We've updated our
Privacy Policy effective December 15. Please read our updated Privacy Policy and tap

学習ガイド > Intermediate Algebra

Domain and Range

4.3 Learning Objectives

  • Find the domain of a square root and rational function
  • Find the domain and range of a function from the algebraic form.
  • Define the domain of linear, quadratic, radical, and rational functions from graphs
Functions are a correspondence between two sets, called the domain and the range. When defining a function, you usually state what kind of numbers the domain (x) and range (f(x)) values can be. But even if you say they are real numbers, that doesn’t mean that all real numbers can be used for x. It also doesn’t mean that all real numbers can be function values, f(x). There may be restrictions on the domain and range. The restrictions partly depend on the type of function. In this topic, all functions will be restricted to real number values. That is, only real numbers can be used in the domain, and only real numbers can be in the range. There are two main reasons why domains are restricted.
  • You can’t divide by 0.
  • You can’t take the square (or other even) root of a negative number, as the result will not be a real number.
In what kind of functions would these two issues occur?
  • the function is a rational function and the denominator is 0 for some value or values of x, [latex]f\left(x\right)=\frac{x+1}{2-x}[/latex] is a rational function
  • the function is a radical function with an even index (such as a square root), and the radicand can be negative for some value or values of x. [latex]f\left(x\right)=\sqrt{7-x}[/latex] is a radical function
The following table gives examples of domain restrictions for several different rational functions.
Function Notes
[latex] f(x)=\frac{1}{x}[/latex] If [latex]x=0[/latex], you would be dividing by 0, so [latex]x\neq0[/latex].
[latex] f(x)=\frac{2+x}{x-3}[/latex] If [latex]x=3[/latex], you would be dividing by 0, so [latex]x\neq3[/latex].
[latex] f(x)=\frac{2(x-1)}{x-1}[/latex] Although you can simplify this function to [latex]f(x)=2[/latex], when [latex]x=1[/latex] the original function would include division by 0. So [latex]x\neq1[/latex].
[latex] f(x)=\frac{x+1}{{{x}^{2}}-1}[/latex] Both [latex]x=1[/latex] and [latex]x=−1[/latex] would make the denominator 0. Again, this function can be simplified to [latex] f(x)=\frac{1}{x-1}[/latex], but when [latex]x=1[/latex] or [latex]x=−1[/latex] the original function would include division by 0, so [latex]x\neq1[/latex] and [latex]x\neq−1[/latex].
[latex] f(x)=\frac{2(x-1)}{{{x}^{2}}+1}[/latex] This is an example with no domain restrictions, even though there is a variable in the denominator. Since [latex]x^{2}\geq0,x^{2}+1[/latex] can never be 0. The least it can be is 1, so there is no danger of division by 0.
Square roots of negative numbers could happen whenever the function has a variable under a radical with an even root. Look at these examples, and note that “square root of a negative variable” doesn’t necessarily mean that the value under the radical sign is negative! For example, if [latex]x=−4[/latex], then [latex]−x=−(−4)=4[/latex], a positive number.
Function Restrictions to the Domain
[latex] f(x)=\sqrt{x}[/latex] If [latex]x<0[/latex], you would be taking the square root of a negative number, so [latex]x\geq0[/latex].
[latex] f(x)=\sqrt{x+10}[/latex] If [latex]x<−10[/latex], you would be taking the square root of a negative number, so [latex]x\geq−10[/latex].
[latex] f(x)=\sqrt{-x}[/latex] When is [latex]-x[/latex] negative? Only when x is positive. (For example, if [latex]x=−3[/latex], then [latex]−x=3[/latex]. If [latex]x=1[/latex], then [latex]−x=−1[/latex].) This means [latex]x\leq0[/latex].
[latex] f(x)=\sqrt{{{x}^{2}}-1}[/latex] [latex]x^{2}–1[/latex] must be positive, [latex]x^{2}–1>0[/latex]. So [latex]x^{2}>1[/latex]. This happens only when x is greater than 1 or less than [latex]−1[/latex]: [latex]x\leq−1[/latex] or [latex]x\geq1[/latex].
[latex] f(x)=\sqrt{{{x}^{2}}+10}[/latex] There are no domain restrictions, even though there is a variable under the radical. Since [latex]x^{2}\ge0[/latex], [latex]x^{2}+10[/latex] can never be negative. The least it can be is [latex]\sqrt{10}[/latex], so there is no danger of taking the square root of a negative number.
So how, exactly do you define the domain of a function anyway?

How To: Given a function written in equation form, find the domain.

  1. Identify the input values.
  2. Identify any restrictions on the input and exclude those values from the domain.
  3. Write the domain in interval form, if possible.

Example 4.3.A

Find the domain of the function [latex]f\left(x\right)={x}^{2}-1[/latex].

Answer: The input value, shown by the variable [latex]x[/latex] in the equation, is squared and then the result is lowered by one. Any real number may be squared and then be lowered by one, so there are no restrictions on the domain of this function. The domain is the set of real numbers. In interval form, the domain of [latex]f[/latex] is [latex]\left(-\infty ,\infty \right)[/latex].

How To: Given a function written in an equation form that includes a fraction, find the domain.

  1. Identify the input values.
  2. Identify any restrictions on the input. If there is a denominator in the function’s formula, set the denominator equal to zero and solve for [latex]x[/latex] . If the function’s formula contains an even root, set the radicand greater than or equal to 0, and then solve.
  3. Write the domain in interval form, making sure to exclude any restricted values from the domain.

Example 4.3.B

Find the domain of the function [latex]f\left(x\right)=\frac{x+1}{2-x}[/latex].

Answer: When there is a denominator, we want to include only values of the input that do not force the denominator to be zero. So, we will set the denominator equal to 0 and solve for [latex]x[/latex].

[latex]\begin{cases}2-x=0\hfill \\ -x=-2\hfill \\ x=2\hfill \end{cases}[/latex]

Now, we will exclude 2 from the domain. The answers are all real numbers where [latex]x<2[/latex] or [latex]x>2[/latex]. We can use a symbol known as the union, [latex]\cup [/latex], to combine the two sets. In interval notation, we write the solution: [latex]\left(\mathrm{-\infty },2\right)\cup \left(2,\infty \right)[/latex].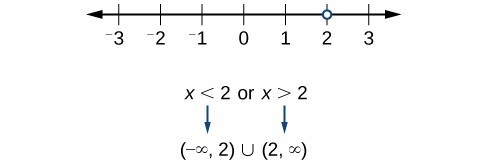
Line graph of x=!2. Figure 3
In interval form, the domain of [latex]f[/latex] is [latex]\left(-\infty ,2\right)\cup \left(2,\infty \right)[/latex].

https://www.youtube.com/watch?v=v0IhvIzCc_I&feature=youtu.be

How To: Given a function written in equation form including an even root, find the domain.

  1. Identify the input values.
  2. Since there is an even root, exclude any real numbers that result in a negative number in the radicand. Set the radicand greater than or equal to zero and solve for [latex]x[/latex].
  3. The solution(s) are the domain of the function. If possible, write the answer in interval form.

Example 4.3.C

Find the domain of the function [latex]f\left(x\right)=\sqrt{7-x}[/latex].

Answer: When there is an even root in the formula, we exclude any real numbers that result in a negative number in the radicand. Set the radicand greater than or equal to zero and solve for [latex]x[/latex].

[latex]\begin{cases}7-x\ge 0\hfill \\ -x\ge -7\hfill \\ x\le 7\hfill \end{cases}[/latex]

Now, we will exclude any number greater than 7 from the domain. The answers are all real numbers less than or equal to [latex]7[/latex], or [latex]\left(-\infty ,7\right][/latex].

https://www.youtube.com/watch?v=lj_JB8sfyIM&feature=youtu.be There can be functions in which the domain and range do not intersect at all. For example, the function [latex]f\left(x\right)=-\frac{1}{\sqrt{x}}[/latex] has the set of all positive real numbers as its domain but the set of all negative real numbers as its range. As a more extreme example, a function’s inputs and outputs can be completely different categories (for example, names of weekdays as inputs and numbers as outputs, as on an attendance chart), in such cases the domain and range have no elements in common.

4.3.1 Find Domain and Range From a Graph

Finding domain and range of different functions is often a matter of asking yourself, what values can this function not have? Pictures make it easier to visualize what domain and range are, so we will show how to define the domain and range of functions given their graphs. What are the domain and range of the real-valued function [latex]f(x)=x+3[/latex]? This is a linear function. Remember that linear functions are lines that continue forever in each direction.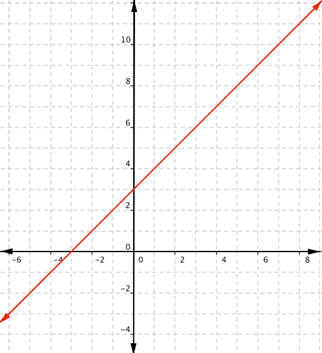 Line for f(x)=x+3 Any real number can be substituted for x and get a meaningful output. For any real number, you can always find an x value that gives you that number for the output. Unless a linear function is a constant, such as [latex]f(x)=2[/latex], there is no restriction on the range. The domain and range are all real numbers. For the examples that follow, try to figure out the domain and range of the graphs before you look at the answer.

Example 4.3.D

What are the domain and range of the real-valued function [latex]f(x)=−3x^{2}+6x+1[/latex]?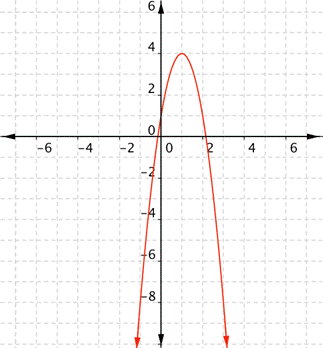 Downward-opening parabola with vertex of 1, 4.

Answer: This is a quadratic function. There are no rational (divide by zero) or radical (negative number under a root) expressions, so there is nothing that will restrict the domain. Any real number can be used for x to get a meaningful output. Because the coefficient of [latex]x^{2}[/latex] is negative, it will open downward. With quadratic functions, remember that there is either a maximum (greatest) value, or a minimum (least) value. In this case, there is a maximum value. The vertex, or high point, is at (1, 4). From the graph, you can see that [latex]f(x)\leq4[/latex].

Answer

The domain is all real numbers, and the range is all real numbers f(x) such that [latex]f(x)\leq4[/latex]. You can check that the vertex is indeed at (1, 4). Since a quadratic function has two mirror image halves, the line of reflection has to be in the middle of two points with the same y value. The vertex must lie on the line of reflection, because it’s the only point that does not have a mirror image! In the previous example, notice that when [latex]x=2[/latex] and when [latex]x=0[/latex], the function value is 1. (You can verify this by evaluating f(2) and f(0).) That is, both (2, 1) and (0, 1) are on the graph. The line of reflection here is [latex]x=1[/latex], so the vertex must be at the point (1, f(1)). Evaluating f(1) gives [latex]f(1)=4[/latex], so the vertex is at (1, 4).

Example 4.3.E

What is the domain and range of the real-valued function [latex]f(x)=-2+\sqrt{x+5}[/latex]?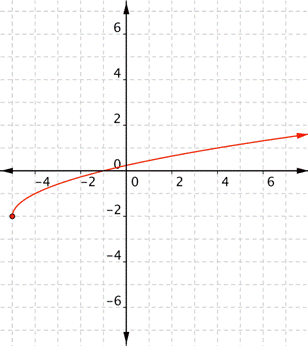 Radical function stemming from negative 5, negative 2.

Answer: This is a radical function. The domain of a radical function is any x value for which the radicand (the value under the radical sign) is not negative. That means [latex]x+5\geq0[/latex], so [latex]x\geq−5[/latex]. Since the square root must always be positive or 0, [latex] \displaystyle \sqrt{x+5}\ge 0[/latex]. That means [latex] \displaystyle -2+\sqrt{x+5}\ge -2[/latex].

Answer

The domain is all real numbers x where [latex]x\geq−5[/latex], and the range is all real numbers f(x) such that [latex]f(x)\geq−2[/latex].

Example 4.3.F

What is the domain of the real-valued function [latex] \displaystyle f(x)=\frac{3x}{x+2}[/latex]?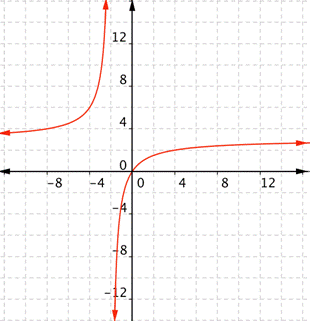 Rational function

Answer: This is a rational function. The domain of a rational function is restricted where the denominator is 0. In this case, [latex]x+2[/latex] is the denominator, and this is 0 only when [latex]x=−2[/latex].

Answer

The domain is all real numbers except [latex]−2[/latex]

In the following video we show how to define the domain and range of functions from their graphs. https://youtu.be/QAxZEelInJc

Summary

Division by 0 could happen whenever the function has a variable in the denominator of a rational expression. That is, it’s something to look for in rational functions. Look at these examples, and note that “division by 0” doesn’t necessarily mean that x is 0! Although a function may be given as “real valued,” it may be that the function has restrictions to its domain and range. There may be some real numbers that can’t be part of the domain or part of the range. This is particularly true with rational and radical functions, which can have restrictions to domain, range, or both. Other functions, such as quadratic functions and polynomial functions of even degree, also can have restrictions to their range.

Licenses & Attributions

CC licensed content, Original

CC licensed content, Shared previously

  • College Algebra. Provided by: OpenStax Located at: https://openstax.org/books/precalculus/pages/1-introduction-to-functions. License: CC BY: Attribution. License terms: Download for Free at: http://cnx.org/contents/[email protected].
  • Unit 17: Functions, from Developmental Math: An Open Program. Provided by: Monterey Institute of Technology and Education Located at: https://www.nroc.org/. License: CC BY: Attribution.
  • Ex 1: Determine the Domain and Range of the Graph of a Function. Authored by: James Sousa (Mathispower4u.com) for Lumen Learning. License: CC BY: Attribution.