We've updated our
Privacy Policy effective December 15. Please read our updated Privacy Policy and tap

Study Guides > Boundless Calculus

Applications of Differentiation

Linear Approximation

A linear approximation is an approximation of a general function using a linear function.

Learning Objectives

Estimate a function's output using linear approximation

Key Takeaways

Key Points

  • By taking the derivative one may find the slope of a function.
  • The values between two points can be approximated as lying on a straight line between those points, where the line is tangent to the function at one of the points.
  • Linear approximation can be made arbitrarily accurate by decreasing the distance between the sample points.

Key Terms

  • linear: having the form of a line; straight
  • differentiable: having a derivative, said of a function whose domain and co-domain are manifolds
In mathematics, a linear approximation is an approximation of a general function using a linear function (more precisely, an affine function). Linear approximations are widely used to solve (or approximate solutions to) equations. Linear approximation is achieved by using Taylor's theorem to approximate the value of a function at a point. Given a twice continuously differentiable function [latex]f[/latex] of one real variable, Taylor's theorem states that: [latex-display]f(x)=f(a)+f'(a)(x-a)+R_2[/latex-display] where [latex]R_2[/latex] is the remainder term (the difference between the actual value of [latex]f(x)[/latex] and the approximation found by the addition of the first two terms). The linear approximation is obtained by dropping the remainder: [latex-display]f(x)=f(a)+f'(a)(x-a)[/latex-display] This is a good approximation for [latex]x[/latex] when it is close enough to [latex]a[/latex]; since a curve, when observed on a smaller and smaller scale, will begin to resemble a straight line. Therefore, the expression on the right-hand side is just the equation for the tangent line to the graph of [latex]f[/latex] at [latex](a, f(a))[/latex]. For this reason, this process is also called the tangent line approximation. If [latex]f[/latex] is concave-down in the interval between [latex]x[/latex] and [latex]a[/latex], the approximation will be an overestimate (since the derivative is decreasing in that interval). If [latex]f[/latex] is concave-up, the approximation will be an underestimate. Since the line tangent to the graph is given by the derivative, differentiation is useful for finding the linear approximation. If one were to take an infinitesimally small step size for [latex]a[/latex], the linear approximation would exactly match the function. Linear approximations for vector functions of a vector variable are obtained in the same way, with the derivative at a point replaced by the Jacobian matrix. For example, given a differentiable function with real values, one can approximate for close to by the following formula: [latex-display]\displaystyle{f(x,y)~f(a,b)+\frac{df}{dx}(a,b)(x-a)+\frac{df}{dy}(a,b)(y-b)}[/latex-display]

Maximum and Minimum Values

Maxima and minima are critical points on graphs and can be found by the first derivative and the second derivative.

Learning Objectives

Use the first and second derivative to find critical points (maxima and minima) on graphs of functions

Key Takeaways

Key Points

  • The critical point of a function is a value for which the first derivative of the function is 0, or undefined.
  • A critical point often indicates a maximum or a minimum, or the endpoint of an interval.
  • If the second derivative at a critical point is positive then it is a minimum, and if it is negative then it is a maximum.

Key Terms

  • critical point: a maximum, minimum, or point of inflection on a curve; a point at which the derivative of a function is zero or undefined
In mathematics, the maximum and minimum (plural: maxima and minima) of a function, known collectively as extrema (singular: extremum), are the largest and smallest value that the function takes at a point either within a given neighborhood (local or relative extremum) or on the function domain in its entirety (global or absolute extremum).
image

Maxima and Minima: Local and global maxima and minima for [latex]\cos \frac{3πx}{x}[/latex], [latex]0.1 \leq x \leq 1.1[/latex].

A real-valued function [latex]f[/latex] defined on a real line is said to have a local (or relative) maximum point at the point [latex]x_{\text{max}}[/latex], if there exists some [latex]\varepsilon > 0[/latex] such that [latex]f(x_{\text{max}}) \geq f(x)[/latex] when [latex]\left | x - x_{\text{max}} \right | < \varepsilon[/latex]. The value of the function at this point is called maximum of the function. Similarly, a function has a local minimum point at [latex]x_{\text{min}}[/latex], if [latex]f(x_{\text{min}}) \leq f(x)[/latex] when [latex]\left | x - x_{\text{min}} \right | < \varepsilon[/latex]. The value of the function at this point is called minimum of the function. A function has a global (or absolute) maximum point at [latex]x_{\text{MAX}}[/latex] if [latex]f(x_{\text{MAX}}) \geq f(x)[/latex] for all [latex]x[/latex]. Similarly, a function has a global (or absolute) minimum point at [latex]x_{\text{MIN}}[/latex] if [latex]f(x_{\text{MIN}}) \leq f(x)[/latex] for all [latex]x[/latex]. The global maximum and global minimum points are also known as the arg max and arg min: the argument (input) at which the maximum (respectively, minimum) occurs. Finding global maxima and minima is the goal of mathematical optimization. If a function is continuous on a closed interval, then by the extreme value theorem global maxima and minima exist. Furthermore, a global maximum (or minimum) either must be a local maximum (or minimum) in the interior of the domain, or must lie on the boundary of the domain. So a method of finding a global maximum (or minimum) is to look at all the local maxima (or minima) in the interior, and also look at the maxima (or minima) of the points on the boundary; and take the biggest (or smallest) one. Local extrema can be found by Fermat's theorem, which states that they must occur at critical points. One can distinguish whether a critical point is a local maximum or local minimum by using the first derivative test or second derivative test.

The Mean Value Theorem, Rolle's Theorem, and Monotonicity

The MVT states that for a function continuous on an interval, the mean value of the function on the interval is a value of the function.

Learning Objectives

Use the Mean Value Theorem and Rolle's Theorem to reach conclusions about points on continuous and differentiable functions

Key Takeaways

Key Points

  • In calculus, the mean value theorem states, roughly: given a planar arc between two endpoints, there is at least one point at which the tangent to the arc is parallel to the secant through its endpoints.
  • More precisely, if a function [latex]f[/latex] is continuous on the closed interval [latex][a, b][/latex], where [latex]a < b[/latex], and differentiable on the open interval [latex](a, b)[/latex], then there exists a point [latex]c[/latex] in [latex](a, b)[/latex] such that [latex]f'(c)=\frac{f(b)-f(a)}{b-a}[/latex].
  • Rolle's Theorem states that if a real-valued function [latex]f[/latex] is continuous on a closed interval [latex][a, b][/latex], differentiable on the open interval [latex](a, b)[/latex], and [latex]f(a) = f(b)[/latex], then there exists a point [latex]c[/latex] in the open interval [latex](a, b)[/latex] such that [latex]f'(c)=0[/latex].

Key Terms

  • mean: The average value.
  • secant: a straight line that intersects a curve at two or more points
  • tangent: a straight line touching a curve at a single point without crossing it there
In calculus, the mean value theorem states, roughly: given a planar arc between two endpoints, there is at least one point at which the tangent to the arc is parallel to the secant through its endpoints.
image

Mean Value Theorem: For any function that is continuous on [latex][a, b][/latex] and differentiable on [latex](a, b)[/latex] there exists some [latex]c[/latex] in the interval [latex](a, b)[/latex] such that the secant joining the endpoints of the interval [latex][a, b][/latex] is parallel to the tangent at [latex]c[/latex].

The theorem is used to prove global statements about a function on an interval starting from local hypotheses about derivatives at points of the interval. More precisely, if a function [latex]f[/latex] is continuous on the closed interval [latex][a, b][/latex], where [latex]a < b[/latex], and differentiable on the open interval [latex](a, b)[/latex], then there exists a point [latex]c[/latex] in [latex](a, b)[/latex] such that [latex-display]\displaystyle{f'(c)=\frac{f(b)-f(a)}{b-a}}[/latex-display] This theorem can be understood intuitively by applying it to motion: If a car travels one hundred miles in one hour, then its average speed during that time was 100 miles per hour. To get at that average speed, the car either has to go at a constant 100 miles per hour during that whole time, or, if it goes slower at one moment, it has to go faster at another moment as well (and vice versa), in order to still end up with an average of 100 miles per hour. Therefore, the Mean Value Theorem tells us that at some point during the journey, the car must have been traveling at exactly 100 miles per hour; that is, it was traveling at its average speed. The mean value theorem follows from the more specific statement of Rolle's theorem, and can be used to prove the more general statement of Taylor's theorem (with Lagrange form of the remainder term). Rolle's Theorem states that if a real-valued function [latex]f[/latex] is continuous on a closed interval [latex][a, b][/latex], differentiable on the open interval [latex](a, b)[/latex], and f(a) = f(b), then there exists a c in the open interval [latex](a, b)[/latex] such that [latex]f'(c)=0[/latex].

Derivatives and the Shape of the Graph

The shape of a graph may be found by taking derivatives to tell you the slope and concavity.

Learning Objectives

Sketch the shape of a graph by using differentiation to find the slope and concavity

Key Takeaways

Key Points

  • The derivative of a function is the the function that defines the slope of the graph at each point.
  • The second derivative of the graph tells you the concavity of the graph at a point.
  • Inflection points are where the second derivative is 0 and are points where the concavity changes.

Key Terms

  • concave: curved like the inner surface of a sphere or bowl
  • convex: curved or bowed outward like the outside of a bowl or sphere or circle
Differentiation is a method to compute the rate at which a dependent output [latex]y[/latex] changes with respect to the change in the independent input [latex]x[/latex]. This rate of change is called the derivative of [latex]y[/latex] with respect to [latex]x[/latex]. In more precise language, the dependence of [latex]y[/latex] upon [latex]x[/latex] means that [latex]y[/latex] is a function of [latex]x[/latex]. This functional relationship is often denoted [latex]y=f(x)[/latex], where [latex]f[/latex] denotes the function. If [latex]x[/latex] and y are real numbers, and if the graph of [latex]y[/latex] is plotted against [latex]x[/latex], the derivative measures the slope of this graph at each point. The simplest case is when [latex]y[/latex] is a linear function of [latex]x[/latex], meaning that the graph of [latex]y[/latex] divided by [latex]x[/latex] is a straight line. In this case, [latex]y=f(x) = m \cdot x+b[/latex], for real numbers [latex]m[/latex] and [latex]b[/latex], and the slope m is given by [latex]\frac{\Delta y}{\Delta x}[/latex], where the symbol [latex]\Delta[/latex] (the uppercase form of the Greek letter Delta) is an abbreviation for "change in. " This formula is true because: [latex-display]y + \Delta y [/latex-display] [latex-display]= f(x+ \Delta x) [/latex-display] [latex-display]= m (x + \Delta x) + b [/latex-display] [latex-display]= m (x + \Delta x) + b [/latex-display] [latex-display]= y + m \Delta x[/latex-display] It follows that: [latex-display]\Delta y = m \Delta x[/latex-display] This gives an exact value for the slope of a straight line. If the function [latex]f[/latex] is not linear (i.e. its graph is not a straight line), however, then the change in [latex]y[/latex] divided by the change in [latex]x[/latex] varies: differentiation is a method to find an exact value for this rate of change at any given value of [latex]x[/latex].

Inflection Point

A point where the second derivative of a function changes sign is called an inflection point. At an inflection point, the second derivative may be zero, as in the case of the inflection point [latex]x=0[/latex] of the function [latex]y=x^3[/latex], or it may fail to exist, as in the case of the inflection point [latex]x=0[/latex] of the function [latex]y=x^{\frac{1}{3}}[/latex]. At an inflection point, a function switches from being a convex function to being a concave function or vice versa.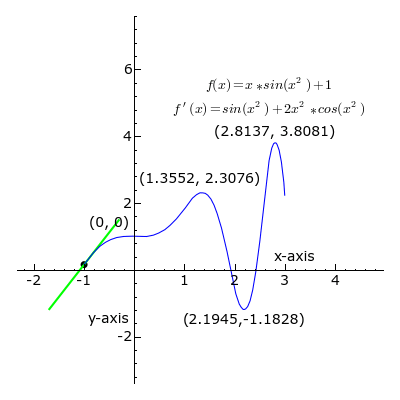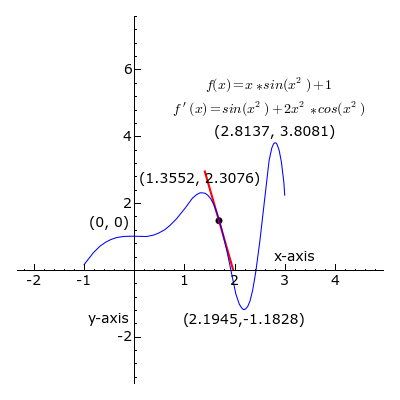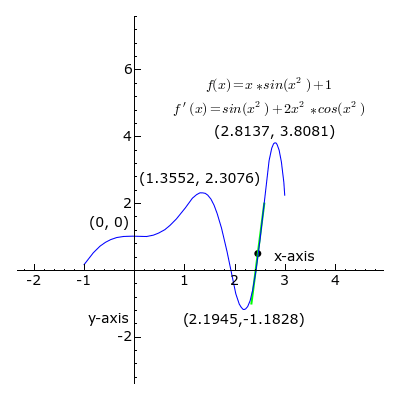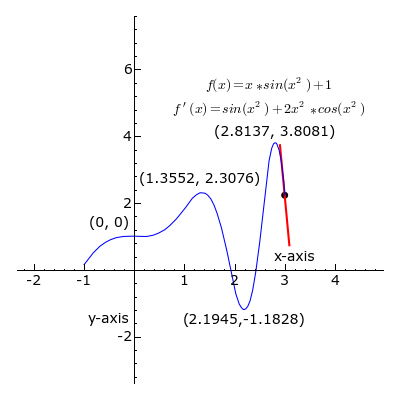
image

Derivative: At each point, the derivative of is the slope of a line that is tangent to the curve. The line is always tangent to the blue curve; its slope is the derivative. Note derivative is positive where a green line appears, negative where a red line appears, and zero where a black line appears.

Horizontal Asymptotes and Limits at Infinity

The asymptotes are computed using limits and are classified into horizontal, vertical and oblique depending on the orientation.

Learning Objectives

Distinguish three types of asymptotes, identifying curves that can and can not have them

Key Takeaways

Key Points

  • Horizontal asymptotes are horizontal lines that the graph of the function approaches as [latex]x[/latex] tends toward [latex]+ \infty[/latex] or [latex]- \infty[/latex].
  • Vertical asymptotes are vertical lines (perpendicular to the [latex]x[/latex]-axis) near which the function grows without bound.
  • Oblique asymptotes are diagonal lines so that the difference between the curve and the line approaches [latex]0[/latex] as [latex]x[/latex] tends toward [latex]+ \infty[/latex] or [latex]- \infty[/latex].

Key Terms

  • limit: a value to which a sequence or function converges
  • arctangent: Any of several single-valued or multivalued functions that are inverses of the tangent function.
The asymptotes are most commonly encountered in the study of calculus of curves of the form [latex]y = ƒ(x)[/latex]. They can be computed using limits and are classified into horizontal, vertical and oblique asymptotes depending on the orientation. Horizontal asymptotes are horizontal lines that the graph of the function approaches as [latex]x[/latex] tends toward [latex]+ \infty[/latex] or [latex]- \infty[/latex]. The horizontal line [latex]y = c[/latex]is a horizontal asymptote of the function [latex]y = ƒ(x)[/latex] if [latex]\lim_{x\rightarrow -\infty}f(x)=c[/latex] or [latex]\lim_{x\rightarrow +\infty}f(x)=c[/latex]. In the first case, [latex]ƒ(x)[/latex] has [latex]y = c[/latex] as asymptote when [latex]x[/latex] tends toward [latex]- \infty[/latex], and in the second that [latex]ƒ(x)[/latex] has [latex]y = c[/latex] as an asymptote as [latex]x[/latex] tends toward [latex]+ \infty[/latex].
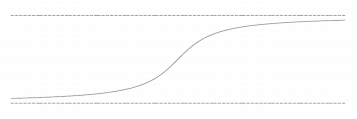
image

Horizontal asymptote: The graph of a function can have two horizontal asymptotes. An example of such a function would be [latex]y = \arctan(x)[/latex].

Vertical asymptotes are vertical lines (perpendicular to the [latex]x[/latex]-axis) near which the function grows without bound. A common example of a vertical asymptote is the case of a rational function at a point [latex]x[/latex] such that the denominator is zero and the numerator is non-zero. Oblique asymptotes are diagonal lines so that the difference between the curve and the line approaches [latex]0[/latex] as [latex]x[/latex] tends toward [latex]+ \infty[/latex] or [latex]- \infty[/latex]. More general type of asymptotes can be defined as the oblique asymptote case. Only open curves that have some infinite branch, can have an asymptote. No closed curve can have an asymptote.

Curve Sketching

Curve sketching is used to produce a rough idea of overall shape of a curve given its equation without computing a detailed plot.

Learning Objectives

Use "curve sketching" to estimate a function's shape

Key Takeaways

Key Points

  • Determine the [latex]x[/latex]- and [latex]y[/latex]-intercepts of the curve.
  • Determine the symmetry of the curve.
  • Determine any bounds on the values of [latex]x[/latex] and [latex]y[/latex].
  • Determine the asymptotes of the curve.

Key Terms

  • symmetry: Exact correspondence on either side of a dividing line, plane, center or axis.
  • asymptote: a straight line which a curve approaches arbitrarily closely, as they go to infinity
In geometry, curve sketching (or curve tracing) includes techniques that can be used to produce a rough idea of overall shape of a plane curve given its equation without computing the large numbers of points required for a detailed plot. It is an application of the theory of curves to find their main features. The following steps are usually easy to carry out and give important clues as to the shape of a curve:
  1. Determine the [latex]x[/latex]- and [latex]y[/latex]-intercepts of the curve. The [latex]x[/latex]-intercepts are found by setting [latex]y[/latex] equal to [latex]0[/latex] in the equation of the curve and solving for [latex]x[/latex]. Similarly, the y intercepts are found by setting [latex]x[/latex] equal to [latex]0[/latex] in the equation of the curve and solving for [latex]y[/latex].
  2. Determine the symmetry of the curve. If the exponent of [latex]x[/latex] is always even in the equation of the curve, then the [latex]y[/latex]- axis is an axis of symmetry for the curve. Similarly, if the exponent of [latex]y[/latex] is always even in the equation of the curve, then the [latex]x[/latex]-axis is an axis of symmetry for the curve. If the sum of the degrees of [latex]x[/latex] and [latex]y[/latex] in each term is always even or always odd, then the curve is symmetric about the origin and the origin is called a center of the curve.
  3. Determine any bounds on the values of [latex]x[/latex] and [latex]y[/latex]. If the curve passes through the origin then determine the tangent lines there. For algebraic curves, this can be done by removing all but the terms of lowest order from the equation and solving. Similarly, removing all but the terms of highest order from the equation and solving gives the points where the curve meets the line at infinity.
  4. Determine the asymptotes of the curve. Also determine from which side the curve approaches the asymptotes and where the asymptotes intersect the curve.

Graphing on Computers and Calculators

Graphics can be created by hand, using computer programs, and with graphing calculators.

Learning Objectives

Demonstrate how computers and calculators can speed up and simplify graphing

Key Takeaways

Key Points

  • A graphing calculator is a handheld scientific calculator capable of plotting graphs, solving simultaneous equations, and performing numerous other tasks with variables.
  • Graphs can be created using open source and proprietary computer programs.
  • High end features of computer programs include speed, high-resolution, and tree-dimensional graphing.

Key Terms

  • proprietary: Manufactured exclusively by the owner of intellectual property rights (IPR), as with a patent or trade secret.
  • scientific calculator: An electronic calculator that can handle trigonometric, exponential and often other advanced functions, and can show its output in scientific notation and sometimes in hexadecimal, octal or binary
  • graph: A diagram displaying data; in particular one showing the relationship between two or more quantities, measurements or indicative numbers that may or may not have a specific mathematical formula relating them to each other.
Graphics can be created by hand using simple everyday tools such as graph paper, pencils, markers, and rulers. However, today they are more often created using computer software, which is often both faster and easier. They can be created with graphing calculators. Graphs are often created using computer software. Both open source computer and proprietary programs can be used for this purpose. For example, GraphCalc (see ) is an open source computer program that runs in Microsoft Windows and Linux that provides the functionality of a graphing calculator. GraphCalc includes many of the standard features of graphing calculators, but also includes some higher-end features.
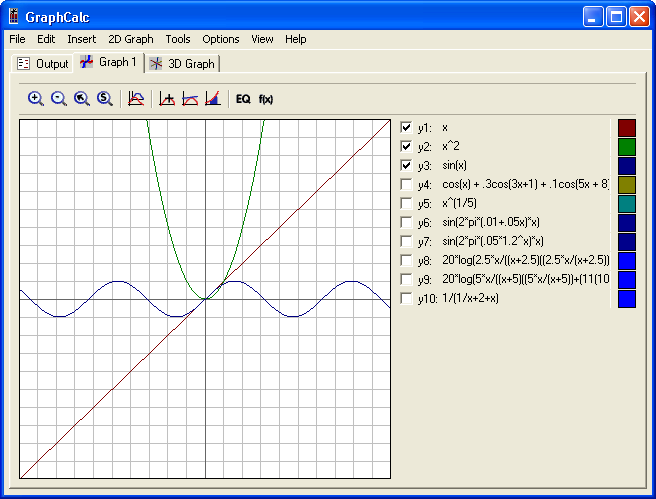
image

GraphCalc: Screenshot of GraphCalc

a) High resolution: Graphing calculator screens have a resolution typically less than 120 by 90 pixels, whereas computer monitors typically display 1280 by 1024 pixels or more. b) Speed: Modern computers are considerably faster than handheld graphing calculators. c) Three-dimensional graphing: While high-end graphing calculators can graph in 3-D, GraphCalc benefits from modern computers' memory, speed, and graphics acceleration. Mathematica is an example of proprietary computational software program used in scientific, engineering, and mathematical fields and other areas of technical computing. It also includes tools for visualizing and analyzing graphs. A graphing calculator (see ) typically refers to a class of handheld scientific calculators that are capable of plotting graphs, solving simultaneous equations, and performing numerous other tasks with variables. Most popular graphing calculators are also programmable, allowing the user to create customized programs, typically for scientific/engineering and education applications. Due to their large displays intended for graphing, they can also accommodate several lines of text and calculations at a time.
image

Graphing Calculator: Calculators graph curves by drawing each pixel as a linear approximation of the function.

Some of the more recent graphing calculators are capable of color output, and also feature animated and interactive drawing of math plots (2D and 3D), other figures such as animated geometry theorems, preparation of documents which can include these plots and drawings, etc. This is giving the new graphing calculators a presence even in high school courses where they were formerly disallowed. Some calculator manufacturers also offer computer software for emulating and working with handheld graphing calculators. Many graphing calculators can be attached to devices like electronic thermometers, pH gauges, weather instruments, decibel and light meters, accelerometers, and other sensors and therefore function as data loggers, as well as WiFi or other communication modules for monitoring, polling and interaction with the teacher. Student laboratory exercises with data from such devices enhances learning of math, especially statistics and mechanics.

Optimization

Mathematical optimization is the selection of a best element (with regard to some criteria) from some set of available alternatives.

Learning Objectives

Define optimization as finding the maxima and minima for a function, and describe its real-life applications

Key Takeaways

Key Points

  • Many design problems can also be expressed as optimization programs.
  • Optimization relies heavily on finding maxima and minima. For this, calculus is useful.
  • An example would be companies seeking to maximize sales while minimizing costs.

Key Terms

  • optimization: the design and operation of a system or process to make it as good as possible in some defined sense
  • stochastic: Random, randomly determined
Mathematical optimization is the selection of a best element (with regard to some criteria) from some set of available alternatives. Optimization process that involves only a single variable is rather straightforward. After finding out the function [latex]f(x)[/latex] to be optimized, local maxima or minima at critical points can be easily found. (Of course, end points may have maximum/minimum values as well.) The same strategy applies for optimization with several variables. Many design problems can also be expressed as optimization programs. This application is called design optimization. One subset is the engineering optimization, and another recent and growing subset of this field is multidisciplinary design optimization, which, while useful in many problems, has in particular been applied to aerospace engineering problems. Economics is closely linked to optimization of agents. Modern optimization theory includes traditional optimization theory but also overlaps with game theory and the study of economic equilibria. In microeconomics, the utility maximization problem and its dual problem, the expenditure minimization problem, are economic optimization problems. Insofar as they behave consistently, consumers are assumed to maximize their utility, while firms are usually assumed to maximize their profit. Also, agents are often modeled as being risk-averse, thereby preferring to avoid risk. Asset prices are also modeled using optimization theory, though the underlying mathematics relies on optimizing stochastic processes rather than on static optimization. Trade theory also uses optimization to explain trade patterns between nations. The optimization of market portfolios is an example of multi-objective optimization in economics. Another field that uses optimization techniques extensively is operations research. Operations research also uses stochastic modeling and simulation to support improved decision-making. Increasingly, operations research uses stochastic programming to model dynamic decisions that adapt to events; such problems can be solved with large-scale optimization and stochastic optimization methods.
image

Maxima: Finding maxima is useful in optimization problems.

Newton's Method

Newton's Method is a method for finding successively better approximations to the roots (or zeroes) of a real-valued function.

Learning Objectives

Use "Newton's Method" to find successively more accurate estimates for a function's [latex]x[/latex]-intercept

Key Takeaways

Key Points

  • Newton's method proceeds by an initial guess which is reasonably close to the true root, then the function is approximated by its tangent line (which can be computed using the tools of calculus).
  • Then compute the [latex]x[/latex]-intercept of this tangent line (which is easily done with elementary algebra). This [latex]x[/latex]-intercept will typically be a better approximation to the function's root than the original guess, and the method can be iterated.
  • The more times you iterate, the more accurate the approximation to the actual roots.

Key Terms

  • derivative: a measure of how a function changes as its input changes
  • root: A zero (of a function).
  • tangent: a straight line touching a curve at a single point without crossing it there
In numerical analysis, Newton's method (also known as the Newton–Raphson method), named after Isaac Newton and Joseph Raphson, is a method for finding successively better approximations to the roots (or zeroes) of a real-valued function. In other words find [latex]x[/latex] such that [latex]f(x)=0[/latex]. Also known as the [latex]x[/latex]-intercept. The Newton-Raphson method in one variable is implemented as follows:
  1. Given a function ƒ defined over the reals x, and its derivative ƒ ', we begin with a first guess x0 for a root of the function f. Provided the function satisfies all the assumptions made in the derivation of the formula, a better approximation x1 is x0 - f(x0) / f'(x0). Geometrically, (x1, 0) is the intersection with the x-axis of a line tangent to f at (x0, f (x0)).The process is repeated as xn+1 = xn - f(xn / f'(xn) until a sufficiently accurate value is reached.
This algorithm is first in the class of Householder's methods, succeeded by Halley's method. The method can also be extended to complex functions and to systems of equations.
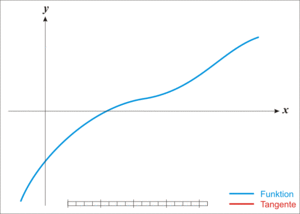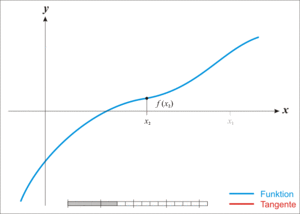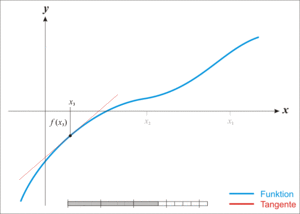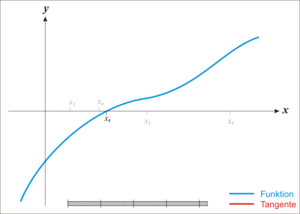
image

Newton's Method: The function [latex]f[/latex] is shown in blue and the tangent line in red. We see that [latex]x_{n+1}[/latex] is a better approximation than [latex]x_n[/latex] for the root [latex]x[/latex] of the function [latex]f[/latex].

The idea of the method is as follows: one starts with an initial guess which is reasonably close to the true root, then the function is approximated by its tangent line (which can be computed using the tools of calculus), and one computes the [latex]x[/latex]-intercept of this tangent line (which is easily done with elementary algebra). This [latex]x[/latex]-intercept will typically be a better approximation to the function's root than the original guess, and the method can be iterated.

Concavity and the Second Derivative Test

The second derivative test is a criterion for determining whether a given critical point is a local maximum or a local minimum.

Learning Objectives

Calculate whether a function has a local maximum or minimum at a critical point using the second derivative test

Key Takeaways

Key Points

  • A critical point is a point where the derivative is 0.
  • If the second derivative is positive, the point is a minimum.
  • If the second derivative is negative, the point is a maximum.
  • If the second derivative is 0, the test is inconclusive.

Key Terms

  • local minimum: A point on a graph (or its associated function) such that the points each side have a greater value even though another point exists with a smaller value.
  • local maximum: A maximum within a restricted domain, especially a point on a function whose value is greater than the values of all other points near it.
  • critical point: a maximum, minimum, or point of inflection on a curve; a point at which the derivative of a function is zero or undefined
In calculus, the second derivative test is a criterion for determining whether a given critical point of a real function of one variable is a local maximum or a local minimum using the value of the second derivative at the point.
image

Maxima and Minima: Telling whether a critical point is a maximum or a minimum has to do with the second derivative. If it is concave-up at the point, it is a minimum; if concave-down, it is a maximum.

The test states: if the function [latex]f[/latex] is twice differentiable at a critical point [latex]x[/latex] (i.e. [latex]f'(x) = 0[/latex]), then: If [latex]f''(x) < 0[/latex] then f(x) has a local maximum at [latex]x[/latex]. If [latex]f''(x) > 0[/latex] then f(x) has a local minimum at [latex]x[/latex]. If [latex]f''(x) = 0[/latex], the test is inconclusive. In the latter case, Taylor's Theorem may be used to determine the behavior of [latex]f[/latex] near [latex]x[/latex] using higher derivatives.

Proof of the Second Derivative Test:

Suppose we have [latex]f''(x) > 0[/latex] (the proof for [latex]f''(x) < 0[/latex] is analogous). By assumption, [latex]f'(x) = 0[/latex]. Then, [latex-display]\displaystyle{0 < f''(x) = \lim_{h \to 0} \frac{f'(x+h)-f'(x)}{h}}[/latex-display] Thus, for a sufficiently small [latex]h[/latex] we get [latex-display]\displaystyle{\frac{f'(x+h)}{h} > 0}[/latex-display] which means that [latex]f'(x+h) < 0[/latex] if [latex]h < 0[/latex] (intuitively, [latex]f[/latex] is decreasing as it approaches [latex]x[/latex] from the left), and that [latex]f'(x+h) > 0[/latex]  if [latex]h > 0[/latex] (intuitively, [latex]f[/latex] is increasing as we go right from [latex]x[/latex]). Now, by the first derivative test, [latex]f(x)[/latex] has a local minimum at [latex]x[/latex]. A related but distinct use of second derivatives is to determine whether a function is concave up or concave down at a point. It does not, however, provide information about inflection points. Specifically, a twice-differentiable function [latex]f[/latex] is concave-up if [latex]f''(x)[/latex] is positive and concave-down if [latex]f''(x)[/latex] is negative.

Differentials

Differentials are the principal part of the change in a function [latex]y = f(x)[/latex] with respect to changes in the independent variable.

Learning Objectives

Use implicit differentiation to find the derivatives of functions that are not explicitly functions of [latex]x[/latex]

Key Takeaways

Key Points

  • Differentials are notated by [latex]dx[/latex] or [latex]dy[/latex].
  • They represent an infinitesimal increase in the variable [latex]x[/latex] or [latex]y[/latex].
  • Higher order differentials represent successive derivatives.

Key Terms

  • infinitesimal: a non-zero quantity whose magnitude is smaller than any positive number
In calculus, the differential represents the principal part of the change in a function [latex]y = f(x)[/latex] with respect to changes in the independent variable. The differential [latex]dy[/latex] is defined by: [latex-display]dy=f'(x)dx[/latex-display] where [latex]f'(x)[/latex] is the derivative of [latex]f[/latex] with respect to [latex]x[/latex], and [latex]dx[/latex] is an additional real variable (so that [latex]dy[/latex] is a function of [latex]x[/latex] and [latex]dx[/latex]). The notation is such that the equation [latex-display]\displaystyle{dy=\frac{dy}{dx}dx}[/latex-display] holds, where the derivative is represented in the Leibniz notation [latex]\frac{dy}{dx}[/latex], and this is consistent regarding the derivative as the quotient of the differentials. One also writes: [latex-display]df (x) = f'(x) dx[/latex-display] The precise meaning of the variables [latex]dy[/latex] and [latex]dx[/latex] depends on the context of the application and the required level of mathematical rigor. The domain of these variables may take on a particular geometrical significance if the differential is regarded as a particular differential form, or a particular analytical significance if the differential is regarded as a linear approximation to the increment of a function. In physical applications, the variables [latex]dx[/latex] and [latex]dy[/latex] are often constrained to be very small ("infinitesimal").
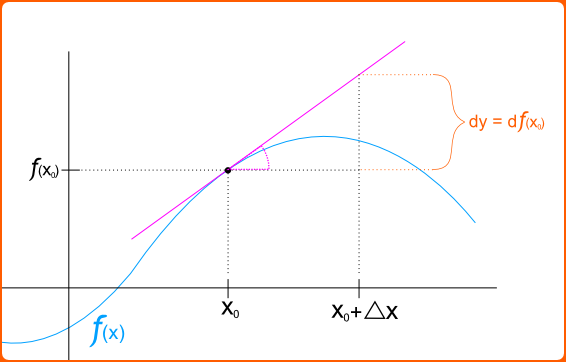
image

Differentials: The differential of a function [latex]f(x)[/latex] at a point [latex]x_0[/latex].

Higher-order differentials of a function [latex]y = f(x)[/latex] of a single variable [latex]x[/latex] can be defined as follows: [latex-display]d(dy)=d(f'(x))[/latex-display] and, in general: [latex-display]\displaystyle{d^n(y)=f^{(n)}(x)(dx)^n}[/latex-display] Informally, this justifies Leibniz's notation for higher-order derivatives. When the independent variable [latex]x[/latex] itself is permitted to depend on other variables, then the expression becomes more complicated, as it must also include higher-order differentials in [latex]x[/latex] itself. Thus, for instance, [latex-display]d^2(y)=f''(x)(dx)^2+f'(x)(d^2x)[/latex-display] and so forth.

Licenses & Attributions

CC licensed content, Shared previously

CC licensed content, Specific attribution