We've updated our
Privacy Policy effective December 15. Please read our updated Privacy Policy and tap

Study Guides > Boundless Algebra

Working With Lines

The Distance Formula and Midpoints of Segments

The distance and the midpoint formulas give us the tools to find important information about two points.

Learning Objectives

Calculate the midpoint of a line segment and the distance between two points on a plane

Key Takeaways

Key Points

  • The Pythagorean Theorem relates the lengths of the three sides of a right triangle.  If [latex]c[/latex] is the hypotenuse and [latex]a[/latex] and [latex]b[/latex] are the other two sides, then [latex]c^{2}=a^{2}+b^{2}[/latex].
  • Using the Pythagorean Theorem and two points [latex](x_{1},y_{1})[/latex] and [latex](x_{2},y_{2})[/latex], we can derive the distance formula: [latex]d=\sqrt{(x_{2}-x_{1})^{2}+(y_{2}-y_{1})^{2}}[/latex].
  • The midpoint of a line segment given by two points [latex](x_{1},y_{1})[/latex] and [latex](x_{2},y_{2})[/latex] is [latex](\frac{x_{1}+x_{2}}{2}, \frac{y_{1}+y_{2}}{2})[/latex].

Key Terms

  • distance: The amount of space between two points, measured along a straight line
  • Pythagorean Theorem: States that the square of the hypotenuse is equal to the sum of the squares of the other two sides in a right triangle.
  • midpoint: A point which divides a line segment into two lines of equal length

The Distance Formula

In analytic geometry, the distance between two points of the [latex]xy[/latex]-plane can be found using the distance formula.  The distance can be from two points on a line or from two points on a line segment.  The distance between points [latex](x_{1},y_{1})[/latex] and [latex](x_{2},y_{2})[/latex] is given by the formula: [latex]\displaystyle d=\sqrt{(x_{2}-x_{1})^{2}+(y_{2}-y_{1})^{2}}[/latex] This formula is easily derived by constructing a right triangle with the hypotenuse connecting the two points ([latex]c[/latex]) and two legs drawn from the each of the two points to intersect each other ([latex]a[/latex] and [latex]b[/latex]), (see image below) and applying the Pythagorean theorem. This theorem states that in any right triangle, the square of the hypotenuse is equal to the sum of the squares of the other two sides.
image Pythagorean Theorem: The Pythagorean Theorem states that the square of the hypotenuse is equal to the sum of the squares of the other two sides.

The image below names the two points, with the distance between them as the variable, [latex]d[/latex].  Notice that the length between each point and the triangle's right angle is found by calculating the difference between the [latex]y[/latex]-coordinates and [latex]x[/latex]-coordinates, respectively.  The distance formula includes the lengths of the legs of the triangle (normally labeled [latex]a[/latex] and [latex]b[/latex]), with the expressions [latex](y_{2}-y_{1})[/latex] and [latex](x_{2}-x_{1})[/latex].

image Distance Formula: The distance formula between two points, [latex](x_{1},y_{1})[/latex] and [latex](x_{2},y_{2})[/latex], shown as the hypotenuse of a right triangle

Example:  Find the distance between the points [latex](2,4)[/latex] and [latex](5,8)[/latex]

Substitute the values into the distance formula that is derived from the Pythagorean Theorem: [latex]\displaystyle d=\sqrt{(x_{2}-x_{1})^{2}+(y_{2}-y_{1})^{2}}[/latex] [latex]\displaystyle \begin{align} d&=\sqrt{(5-2)^{2}+(8-4)^{2}}\\&=\sqrt{3^{2}+4^{2}}\\&=\sqrt{25}\\&=5 \end{align}[/latex]

Midpoint of a Line Segment

In geometry, the midpoint is the middle point of a line segment, or the middle point of two points on a line, and thus is equidistant from both end-points. If you have two points, [latex](x_{1},y_{1})[/latex] and [latex](x_{2},y_{2})[/latex], the midpoint of the segment connecting the two points can be found with the formula: [latex]\displaystyle (\frac{x_{1}+x_{2}}{2}, \frac{y_{1}+y_{2}}{2})[/latex] Another way to interpret this formula is an average: we average the [latex]x[/latex]-coordinates to find the [latex]x[/latex]-coordinate of the midpoint, and we average the [latex]y[/latex]-coordinates to find the [latex]y[/latex]-coordinate of the midpoint. By looking at each coordinate, you can see that the [latex]x[/latex]-coordinate is halfway between [latex]x_{1}[/latex] and [latex]x_{2}[/latex], and the [latex]y[/latex]-coordinate is halfway between [latex]y_{1}[/latex] and [latex]y_{2}[/latex].
image Midpoint of a Line Segment: The equation for a midpoint of a line segment with endpoints [latex](x_{1},y_{1})[/latex]and [latex](x_{2},y_{2})[/latex]

Example:  Find the midpoint between [latex](2,4) [/latex] and [latex](5,8)[/latex]

Substitute the values into the midpoint formula: [latex]\displaystyle \begin{align} (\frac{x_{1}+x_{2}}{2}, \frac{y_{1}+y_{2}}{2})&=(\frac{2+5}{2}, \frac{4+8}{2})\\&=(\frac{7}{2}, 6) \end{align}[/latex]

Parallel and Perpendicular Lines

Parallel lines never intersect; perpendicular lines intersect at right angles.

Learning Objectives

Practice finding equations for lines that are parallel and lines that are perpendicular

Key Takeaways

Key Points

  • Any two lines are parallel if they have the same slope.
  • Two lines in the same plane are perpendicular if their slopes are negative reciprocals of each other. This means that one has slope of [latex]m[/latex] and the other has a slope of [latex]-\frac{1}{m}[/latex].
  • Two lines in the same plane are perpendicular if the product of their slopes equals [latex]-1[/latex].

Key Terms

  • parallel lines: Lines which never intersect even as they go to infinity. Their slopes are equal to each other.
  • reciprocal: Of a number, the number obtained by dividing [latex]1[/latex] by the given number; the result of exchanging the numerator and the denominator of a fraction.
  • perpendicular lines: Two lines whose intersection creates right angles. Their slopes are the negative reciprocal of each other.

Parallel Lines

Two lines in a plane that do not intersect or touch at a point are called parallel lines. The parallel symbol is [latex]\parallel[/latex]. For example, given two lines: [latex]f(x)=m_{1}x+b_{1}[/latex]and [latex]g(x)=m_{2}x+b_{2}[/latex], writing [latex]f(x)[/latex] [latex]\parallel[/latex] [latex]g(x)[/latex] states that the two lines are parallel to each other.  In 2D, two lines are parallel if they have the same slope. Given two parallel lines [latex]f(x)[/latex] and [latex]g(x)[/latex], the following is true:
  1. Every point on [latex]f(x)[/latex] is located at exactly the same minimum distance from [latex]g(x)[/latex].
  2. Line [latex]f(x)[/latex] is on the same plane as [latex]g(x)[/latex] but does not intersect [latex]g(x)[/latex], even assuming that the two lines extend to infinity in either direction.
Recall that the slope-intercept form of an equation is: [latex]y=mx+b[/latex] and the point-slope form of an equation is: [latex]y-y_{1}=m(x-x_{1})[/latex], both contain information about the slope, namely the constant [latex]m[/latex]. If two lines, say [latex]f(x)=mx+b[/latex] and [latex]g(x)=nx+c[/latex], are parallel, then [latex]n[/latex] must equal [latex]m[/latex]. For example, in the graph below, [latex]f(x)=2x+3[/latex] and [latex]g(x)=2x-1[/latex] are parallel since they have the same slope, [latex]m=2[/latex].
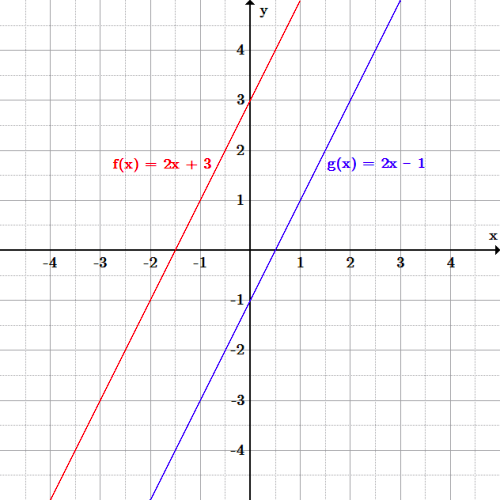image Parallel lines: [latex]f(x)=2x+3[/latex] in red is parallel to [latex]g(x)=2x-1[/latex] in blue; the slopes obtained from the graphs of the lines is the same as the slopes in their equations.

Perpendicular Lines

Two lines are perpendicular to each other if they form congruent adjacent angles. In other words, they are perpendicular if the angles at their intersection are right angles, [latex]90[/latex] degrees. The perpendicular symbol is [latex]\perp[/latex]. For example given two lines, [latex]f(x)=m_{1}x+b_{1}[/latex] and [latex]g(x)=m_{2}x+b_{2}[/latex], writing[latex]f(x)\perp g(x)[/latex] states that the two lines are perpendicular to each other. For two lines in a 2D plane to be perpendicular, their slopes must be negative reciprocals of one another, or the product of their slopes must equal [latex]-1[/latex].  This means that if the slope of one line is [latex]m[/latex], then the slope of its perpendicular line is [latex]\frac{-1}{m}[/latex]. The two slopes multiplied together must equal [latex]-1[/latex]. However, this method cannot be used if the slope is zero or undefined (the line is parallel to an axis). Given two lines: [latex]f(x)=3x-2[/latex] and [latex]g(x)=\frac{-1}{3}x+1[/latex], note the values of the slopes.  Since [latex]3[/latex] is the negative reciprocal of [latex]-\frac{1}{3}[/latex], the two lines are perpendicular. Also, the product of the slopes equals [latex]-1[/latex].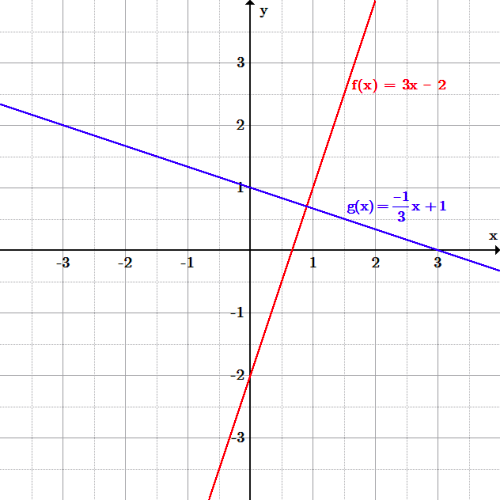
image Perpendicular lines: The line [latex]f(x)=3x-2[/latex] in red is perpendicular to line [latex]g(x)=\frac{-1}{3}x+1[/latex] in blue. The values of their slopes are negative reciprocals of each other; therefore, the angle of intersection is [latex]90[/latex] degrees.

Writing Equations of Parallel and Perpendicular Lines

Example:  Write an equation of the line (in slope-intercept form) that is parallel to the line [latex]y=-2x+4[/latex] and passes through the point [latex](-1,1)[/latex]

Start with the equation for slope-intercept form and then substitute the values for the slope and the point, and solve for [latex]b[/latex]: [latex]y=mx+b[/latex].  The value of the slope will be equal to the current line, since the new line is parallel to it.  The point [latex](-1,1)[/latex] is substituted for [latex](x,y)[/latex]. [latex]\displaystyle y=mx+b[/latex] [latex]\displaystyle \begin{align} 1&=-2(-1)+b\\ \\ 1&=2+b\\ \\ b&=-1 \end{align}[/latex] Therefore, the equation of the line has a slope ([latex]m[/latex]) of [latex]-2[/latex] and a [latex]y[/latex]-intercept ([latex]b[/latex]) of [latex]-1[/latex].  The equation is [latex]y=-2x-1[/latex].

Example:  Write an equation of the line (in slope-intercept form) that is perpendicular to the line [latex]y=\frac{1}{4}x-3[/latex] and passes through the point [latex](2,4)[/latex]

Again, start with the slope-intercept form and substitute the values, except the value for the slope will be the negative reciprocal.  The negative reciprocal of [latex]\frac{1}{4}[/latex] is [latex]-4[/latex].  Therefore, the new equation has a slope of [latex]-4[/latex], through the point [latex](2,4)[/latex].  Solve for [latex]b[/latex]. [latex-display]y=mx+b[/latex-display] [latex]\displaystyle \begin{align} 4&=-4(2)+b\\ \\ 4&=-8+b\\ \\ b&=12 \end{align}[/latex] Therefore, the equation of the line perpendicular to the given line has a slope of [latex]-4[/latex] and a [latex]y[/latex]-intercept of [latex]12[/latex].  The equation is [latex]y=-4x+12[/latex].

Linear Inequalities

A linear inequality is an expression that is designated as less than, greater than, less than or equal to, or greater than or equal to.

Learning Objectives

Solve problems involving linear inequalities

Key Takeaways

Key Points

  • When two expressions are connected by any of the following signs: [latex]<[/latex], [latex]>[/latex], [latex]\leq[/latex], [latex]\geq[/latex], or [latex]\ne[/latex] we have an inequality. For inequalities that contain variable expressions, you may be asked to solve the inequality for that variable. This just means that you need to find the values of the variable that make the inequality true.
  • A linear inequality is solved very similarly to how we solve equations. The difference is that the answers are more than one true value, they can be any of the following: [latex]<[/latex], less than the found solution, [latex]>[/latex], greater than the found solution [latex]\leq[/latex], contains values equal and less than the found solution, [latex]\geq[/latex], contains values equal and greater than the found solution.
  • When you multiply or divide each side of an inequality by a negative number, you must reverse the inequality symbol to maintain a true statement.

Key Terms

  • inequality: A statement that of two quantities of which one is specifically less than or greater than another. Symbols: [latex]<[/latex] or [latex]\leq[/latex] or [latex]>[/latex] or [latex]\geq[/latex], as appropriate.
  • linear equation: A polynomial equation of the first degree (such as [latex]x=2y-7[/latex]).
  • real numbers: The smallest set containing all limits of convergent sequences of rational numbers.

Linear Inequalities

When two linear expressions are not equal, but are designated as less than ([latex]<[/latex]), greater than ([latex]>[/latex]), less than or equal to ([latex]\leq[/latex]) or greater than or equal to ([latex]\geq[/latex]), it is called a linear inequality.  A linear inequality looks exactly like a linear equation, with the inequality sign replacing the equality sign. For inequalities that contain variable expressions, you may be asked to solve the inequality for that variable. This just means that you need to find the values of the variable that make the inequality true. A linear inequality looks like a linear equation, with the inequality sign replacing the equal sign.  The same properties for solving an equation are used to solve an inequality; however, when solving an equation there is one solution (or one value that makes the equation true), but when solving an inequality there are many solutions (or values that make the statement true).

Solutions of Linear Inequalities

Example: Graph the solutions of the inequality: [latex]x>4[/latex]

The solutions to this inequality includes every number that is greater than [latex]4[/latex] as shown below.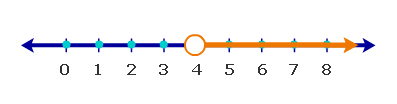
A number line with an open circle on 4 and the numbers to the right of it (greater than 4), shaded in yellow. Inequality: Solutions to [latex]x>4[/latex] are graphed in yellow on the number line.  Notice the open circle means that the value of [latex]4[/latex] in not a solution to the inequality since [latex]4>4[/latex] is a false statement.  If the inequality was [latex]x\geq 4[/latex], then [latex]4[/latex] would be a solution and there would be a closed circle over the [latex]4[/latex] on the number line.

Solving Linear Inequalities

Solving the inequality is the same as solving an equation.  There is only one rule that is different: When you multiply or divide each side of an inequality by a negative number, you must reverse the inequality symbol to maintain a true statement.

Example:  Solve the inequality: [latex]-7x+3+x \leq 1-4x-10[/latex]

Step 1, combine like terms on each side of the inequality symbol: [latex]\displaystyle -6x+3\leq-4x-9[/latex] Step 2, since there is a variable on both sides of the inequality, choose to move the [latex]-4x[/latex], to combine the variables on the left hand side of the inequality. Adding [latex]4x[/latex] yields: [latex]\displaystyle -2x+3\leq-9[/latex] Step 3, this is similar to solving a two step equation. Subtract [latex]3[/latex]: [latex]\displaystyle -2x\leq-12[/latex] Finally, divide both sides by [latex]-2[/latex] (remember to reverse the inequality symbol): [latex]\displaystyle x\ge 6[/latex] To read this answer, read from right to left, [latex]x\geq6[/latex]. This reads "[latex]x[/latex] is greater than or equal to 6".

Licenses & Attributions

CC licensed content, Shared previously

CC licensed content, Specific attribution