Domain and Range
Introduction to Domain and Range
The domain of a function is the set of all possible input values that produce some output value rangeLearning Objectives
Define the domain and range of a functionKey Takeaways
Key Points
- Given a function [latex]f[/latex], the set [latex]x[/latex] values (inputs) is the domain of [latex]f[/latex], and the set [latex]y[/latex] values ( outputs ) is the range of [latex]f[/latex].
- The domain of a function [latex]f[/latex] is all of the values for which the function is defined. For instance, [latex]\frac{1}{x}[/latex] is not defined when [latex]x=0[/latex]. Also, [latex]\sqrt{x}[/latex] is not defined when [latex]x[/latex] is negative.
- To find the domain of a function [latex]f[/latex], you must find the values for which [latex]f[/latex] is not defined. So the domain for [latex]\sqrt{x}[/latex] is [latex] x \geq 0[/latex].
Key Terms
- domain: The set of all points over which a function is defined.
- range: The set of values the function takes on as output.
- function: A relationship between two quantities, called the input and the output; for each input, there is exactly one output.
What Is the Domain and Range of a Function?
The domain of a function is the set of input values, [latex]x[/latex], for which a function is defined. The domain is shown in the left oval in the picture below. The function provides an output value, [latex]f(x)[/latex], for each member of the domain. The set of values the function outputs is termed the range of the function, and those values are shown in the right hand oval in the picture below. A function is the relation that takes the inputs of the domain and output the values in the range. The rule for a function is that for each input there is exactly one output.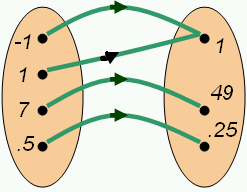 Mapping of a Function: The oval on the left is the domain of the function [latex]f[/latex], and the oval on the right is the range. The green arrows show how each member of the domain is mapped to a particular value of the range.
Mapping of a Function: The oval on the left is the domain of the function [latex]f[/latex], and the oval on the right is the range. The green arrows show how each member of the domain is mapped to a particular value of the range.As you can see in the illustration, each value of the domain has a green arrow to exactly one value of the range. Therefore this mapping is a function.
We can also tell by the set of ordered pairs given in this mapping that it is a function because none of the [latex]x[/latex]-values repeat: [latex](-1,1),(1,1),(7,49),(0.5,0.25)[/latex]; since each input maps to exactly one output. (Note that although the output value of [latex]1[/latex] repeats, only the input values can not repeat) We can also tell this mapping, and set of ordered pairs is a function based on the graph of the ordered pairs because the points do not make a vertical line. If an [latex]x[/latex]value were to repeat there would be two points making a graph of a vertical line, which would not be a function. Let's look at this mapping and list of ordered pairs graphed on a Cartesian Plane. Ordered pairs: This mapping or set of ordered pairs is a function because the points do not make a vertical line. This is called the vertical line test of a function. It shows that for every input there is exactly one output value.
Ordered pairs: This mapping or set of ordered pairs is a function because the points do not make a vertical line. This is called the vertical line test of a function. It shows that for every input there is exactly one output value.In addition, the domain of [latex]f(x)=x^{2}[/latex] is the set of all real numbers, [latex]\mathbb{R}[/latex], as every real number you put into [latex]f[/latex] will give an output, namely [latex] x^2[/latex].
It is important to note that not all functions have the set of real numbers as their domain. For instance, the function [latex]f(x) = \frac{1}{x}[/latex] is not defined for [latex]x=0[/latex], because you cannot divide a number by [latex]0[/latex]. In this case, the domain of [latex]f[/latex] is the set of all real numbers except [latex]0[/latex]. That is, [latex]x\neq0[/latex]. So the domain of this function is [latex]\mathbb{R}-\{0\}[/latex]. What about the function [latex]f(x)=\sqrt{x}[/latex] ? In this case, the square root of a negative number is not defined, and so the domain is the set of all real numbers where [latex]x\geq0[/latex].Finding the Domain and Range: Given a Function
In order to find the domain of a function, if it isn't stated to begin with, we need to look at the function definition to determine what values are not allowed. For instance, we know that you cannot take the square root of a negative number, and you cannot divide by [latex]0[/latex]. With this knowledge in hand, let's find the domain of a function. Example 1: Find the domain of: [latex]\displaystyle f(x)=\frac{1}{\sqrt{x-1}-2}+x[/latex] First, we know we cannot divide by [latex]0[/latex], so any value of [latex]x[/latex] that causes a division by [latex]0[/latex] is not allowed in the domain. In this example, this occurs when: [latex]\displaystyle \sqrt{x-1}-2=0[/latex] Solving for [latex]x[/latex], this happens when [latex]x=5[/latex], so we know that [latex]x\neq5[/latex]. We also know we can't take the square root of a negative number. This means that: [latex]\displaystyle x-1>0 [/latex] After solving for [latex]x[/latex], we see that [latex]x>1[/latex]. So this function's domain is the set of all real numbers such that [latex]x>1[/latex] and [latex]x\neq5[/latex]. Therefore, to find what values are not in the domain, you must find the values where the function is not defined.Visualizing Domain and Range
All values in the domain are mapped onto values in the range that are visualized as graphs of functionsLearning Objectives
Use the graph of a function to determine its domain and rangeKey Takeaways
Key Points
- Values in the domain map onto values in the range.
- The horizontal and vertical line test can help determine the type of relation between the domain and range.
Key Terms
- range: The set of values (points) which a function can obtain.
- domain: The set of all points over which a function is defined.
- function: Any mathematical formula that produces one and only one result for each input.
Review of Domain, Range, and Functions
As stated in a previous section, the domain of a function is the set of 'input' values [latex](x)[/latex] for which the function is defined. The domain is part of the definition of a function. For example, the domain of the function [latex]f(x) = \sqrt{x} [/latex] is [latex]x\geq0[/latex]. The range of a function is the set of results, solutions, or ' output ' values [latex](y)[/latex] to the equation for a given input. By definition, a function only has one result for each domain. For instance, the function [latex]f(x)=x^{2}[/latex] has a range of [latex]f(x)\geq0[/latex], because the square of a number always yields a positive result. In taking both domain and range into account, a function is any mathematical formula that produces one and only one result for each input. Hence, every given domain value has one and only one range value as a result, but not necessarily vice versa. In other words, two different values of [latex]x[/latex] can have the same [latex]y[/latex]-value, but each [latex]y[/latex]-value must be joined with a distinct [latex]x[/latex]-value. This makes sense since results can repeat (the [latex]y[/latex]-values), but inputs cannot (the [latex]x[/latex]-values).Determining Domain and Range
The domain and range can be visualized using a graph, such as the graph for [latex]f(x)=x^{2}[/latex], shown below as a red U-shaped curve. The blue N-shaped (inverted) curve is the graph of [latex]f(x)=-\frac{1}{12}x^3[/latex]. Example 1: Determine the domain and range of each graph pictured below: Both graphs include all real numbers [latex]x[/latex] as input values, since both graphs continue to the left (negative values) and to the right (positive values) for [latex]x[/latex] (inputs). The curves continue to infinity in both directions; therefore, we say the domain for both graphs is the set of all real numbers, notated as: [latex]\mathbb{R}[/latex]. If we now look at the possible outputs or [latex]y[/latex]-values, [latex]f(x)[/latex], (looking up and down the [latex]y[/latex]-axis, notice that the red graph does NOT include [latex]y[/latex]-values that are negative, whereas the blue graph does include both positive and negative values. Therefore, the range for the graph [latex]f(x)=x^{2}[/latex], is [latex]\mathbb{R}[/latex] except [latex]y< 0[/latex], or simply stated: [latex]y \geq 0[/latex]. The range for the graph [latex]f(x)=-\frac{1}{12}x^3[/latex], is [latex]\mathbb{R}[/latex].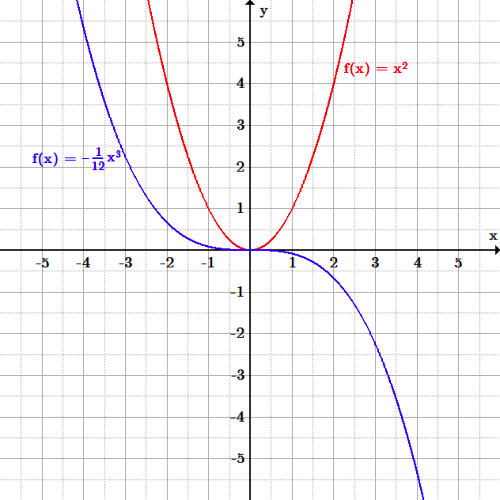 Domain and range graph: The graph of [latex]f(x)=x^2[/latex] (red) has the same domain (input values) as the graph of [latex]f(x)=-\frac{1}{12}x^3[/latex] (blue) since all real numbers can be input values. However, the range of the red graph is restricted to only [latex]f(x)\geq0[/latex], or [latex]y[/latex]-values above or equal to [latex]0[/latex]. The range of the blue graph is all real numbers, [latex]\mathbb{R}[/latex].
Domain and range graph: The graph of [latex]f(x)=x^2[/latex] (red) has the same domain (input values) as the graph of [latex]f(x)=-\frac{1}{12}x^3[/latex] (blue) since all real numbers can be input values. However, the range of the red graph is restricted to only [latex]f(x)\geq0[/latex], or [latex]y[/latex]-values above or equal to [latex]0[/latex]. The range of the blue graph is all real numbers, [latex]\mathbb{R}[/latex].Example 2: Determine the domain and range of each graph pictured below:
 Domain and range graph: The blue graph is the trigonometric function [latex]f(x)=sin (x)[/latex] with a domain of [latex]\mathbb{R}[/latex] and a restricted range of [latex]-1 \leq y \leq 1[/latex] (output values only exist between [latex]-1[/latex] to [latex]1[/latex]. The red graph is the function [latex]f(x)=-\sqrt{x}[/latex] with a restricted domain of [latex]x \geq 0[/latex], and also a restricted range of [latex]y\leq0[/latex].
Domain and range graph: The blue graph is the trigonometric function [latex]f(x)=sin (x)[/latex] with a domain of [latex]\mathbb{R}[/latex] and a restricted range of [latex]-1 \leq y \leq 1[/latex] (output values only exist between [latex]-1[/latex] to [latex]1[/latex]. The red graph is the function [latex]f(x)=-\sqrt{x}[/latex] with a restricted domain of [latex]x \geq 0[/latex], and also a restricted range of [latex]y\leq0[/latex].Domains of Rational and Radical Functions
Rational and radical expressions have restrictions on their domains which can be found algebraically or graphically.Learning Objectives
Calculate the domain of a rational or radical function by finding the values for which it is undefinedKey Takeaways
Key Points
- A rational expression is the quotient of two polynomials. It can be expressed as [latex]\displaystyle \frac{P(x)}{Q(x)}[/latex].
- A rational expression's domain is set such that the denominator cannot equal zero. Therefore, given [latex]\displaystyle \frac{P(x)}{Q(x)}[/latex], [latex]Q(x)\neq 0[/latex].
- To determine the domain of a rational expression, set the denominator equal to zero, then solve for [latex]x[/latex]. All values of [latex]x[/latex] except for those that satisfy [latex]Q(x)=0[/latex] are the domain of the expression.
- A radical expression, is expressed as [latex]\sqrt x[/latex] and can have other roots other than a square root.
- A radical function is expressed as [latex]f(x)=\sqrt x[/latex], (usually just referred to as the "square root function") is a function that maps the set of non-negative real numbers onto itself.
- To determine the domain of a radical expression, set the radicand equal to zero, then solve for [latex]x[/latex]. All values of [latex]x[/latex] except for those that satisfy [latex]\sqrt x=0[/latex] are the domain of the expression.
Key Terms
- radicand: The number or expression underneath the radical sign.
- rational expression: An expression that can be written as the quotient of two polynomials.
Finding Domains of Rational Functions
A rational expression is one which can be written as the ratio of two polynomial functions. Despite being called a rational expression, neither the coefficients of the polynomials nor the values taken by the function are necessarily rational numbers. In the case of one variable, [latex]x[/latex], an expression is called rational if and only if it can be written in the form: [latex]\displaystyle \frac { P(x) }{ Q(x) }[/latex] where [latex]P(x)[/latex] and [latex]Q(x)[/latex] are polynomial functions in [latex]x [/latex] and [latex]Q(x)[/latex] is not the zero polynomial [latex](Q(x) \neq 0)[/latex]. The domain of a rational expression of is the set of all points for which the denominator is not zero. If the denominator of the equation becomes equal to zero, the expression is undefined at that point.Example 1: What is the domain of the rational function:
[latex]\displaystyle f(x)= \frac { x^3-2x }{ 2(x^2-5) }[/latex] To find the domain of a rational function, set the denominator equal to zero and solve. All values of [latex]x[/latex] except for those that satisfy [latex]2(x^2-5)=0[/latex] are the domain of the expression. [latex]\displaystyle 2(x^2-5)=0[/latex] To solve, divide both sides by [latex]2[/latex], add [latex]5[/latex] to both sides, and then take the square root of both sides to yield: [latex]\displaystyle x=\pm \sqrt { 5 }[/latex]. Therefore the domain is the set of all real numbers except the square root of five or negative square root of five. Notice the graph of the function below. At the values of [latex]x=\pm \sqrt { 5 }[/latex] (which is approximately [latex]\pm 2.2[/latex]), the graph does not exist. Rational function with restricted domain: The graph of the function: [latex]f(x)=\displaystyle \frac { x^3-2x }{ 2(x^2-5) }[/latex], where the domain is restricted at [latex]x=\pm \sqrt { 5 }[/latex] since the function does not exist at those points.
Rational function with restricted domain: The graph of the function: [latex]f(x)=\displaystyle \frac { x^3-2x }{ 2(x^2-5) }[/latex], where the domain is restricted at [latex]x=\pm \sqrt { 5 }[/latex] since the function does not exist at those points.Example 2: What is the domain of the rational function:
[latex]\displaystyle f(x)= \frac{\left(x^2-2\right)}{x}[/latex]
Algebraically, the domain is the set of all real numbers except zero, since the denominator can not equal zero. One way to determine this is to look at it graphically. We can see that the graph is discontinuous at [latex]x=0[/latex], indicating that the domain is all numbers other than [latex]x=0[/latex]. This makes sense, because at [latex]x=0[/latex] we would have to divide by zero, which is undefined. The lines of the graph get closer and closer to the value [latex]x=0[/latex], but never touch. Rational Function Dividing by [latex]x[/latex]: A graph of the equation: [latex]f(x)= \frac{\left(x^2-2\right)}{x}[/latex]. To determine the domain of this function, we can graph it and look for where the function doesn't exist, in this case when [latex]x=0[/latex].
Rational Function Dividing by [latex]x[/latex]: A graph of the equation: [latex]f(x)= \frac{\left(x^2-2\right)}{x}[/latex]. To determine the domain of this function, we can graph it and look for where the function doesn't exist, in this case when [latex]x=0[/latex].Finding Domains of Radical Functions
The principal square root function [latex]f(x)=\sqrt x[/latex] (usually just referred to as the "square root function") is a function that maps the set of non-negative real numbers onto itself. Radical Function: The function [latex]f(x)=\sqrt x[/latex] consists of a restricted domain of [latex]x\geq 0[/latex], or non-negative real numbers, since we can not take the square root of a negative number.
Radical Function: The function [latex]f(x)=\sqrt x[/latex] consists of a restricted domain of [latex]x\geq 0[/latex], or non-negative real numbers, since we can not take the square root of a negative number.Note that half of the parabola is missing since functions cannot have more than one value at a point, and the square root function is taken to yield a positive value (though [latex](-x)^2[/latex] gives the same value as [latex]x^2[/latex] so the square root of a number [latex]y[/latex] such that [latex]y=x^2[/latex] would be [latex]\sqrt y = \pm x[/latex]). It is important to remember when graphing the roots that negative values of [latex]x[/latex] will not produce real numbers. This will be explained further in the section on imaginary numbers.
To determine the domain of a radical function algebraically, find the values of [latex]x[/latex] for which the radicand is nonnegative (set it equal to [latex]\geq 0[/latex]) and then solve for [latex]x[/latex]. The radicand is the number or expression underneath the radical sign. All values of [latex]x[/latex] except for those that satisfy [latex]\sqrt x \geq 0[/latex] are the domain of the function.Example 3: What is the domain of the radical function:
[latex]\displaystyle f(x) = \sqrt {x-3} +4[/latex]
Set the radicand greater than or equal to zero and solve for [latex]x[/latex] to find the restrictions on the domain: [latex]\displaystyle {x-3} \geq 0[/latex] Therefore [latex]x \geq 3[/latex]. So, all real number greater than or equal to [latex]3[/latex] is the domain of the function.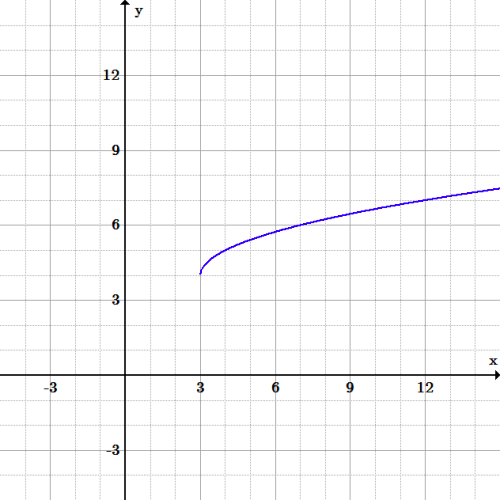 Radical function: The graph of the equation: [latex]f(x) = \sqrt {x-3} +4[/latex]. The function has the domain of all real numbers greater than or equal to [latex]3[/latex], as shown in the graph above.
Radical function: The graph of the equation: [latex]f(x) = \sqrt {x-3} +4[/latex]. The function has the domain of all real numbers greater than or equal to [latex]3[/latex], as shown in the graph above.Licenses & Attributions
CC licensed content, Shared previously
- Curation and Revision. Authored by: Boundless.com. License: Public Domain: No Known Copyright.
CC licensed content, Specific attribution
- range. Provided by: Wikipedia License: CC BY-SA: Attribution-ShareAlike.
- function. Provided by: Wikipedia License: CC BY-SA: Attribution-ShareAlike.
- Algebra/Functions. Provided by: Wikibooks License: CC BY-SA: Attribution-ShareAlike.
- Domain of a function. Provided by: Wikipedia License: CC BY-SA: Attribution-ShareAlike.
- domain. Provided by: Wiktionary License: CC BY-SA: Attribution-ShareAlike.
- Original figure by Julien Coyne. Licensed CC BY-SA 4.0. Provided by: Julien Coyne License: CC BY-SA: Attribution-ShareAlike.
- Allowed mapping for a function. Provided by: Wikibooks License: CC BY-SA: Attribution-ShareAlike.
- function. Provided by: Wikipedia Located at: https://en.wikipedia.org/wiki/Function_(mathematics). License: CC BY-SA: Attribution-ShareAlike.
- Domain and range. Provided by: Wikipedia License: CC BY-SA: Attribution-ShareAlike.
- Algebra/Functions. Provided by: Wikibooks License: CC BY-SA: Attribution-ShareAlike.
- domain. Provided by: Wiktionary License: CC BY-SA: Attribution-ShareAlike.
- range. Provided by: Wiktionary License: CC BY-SA: Attribution-ShareAlike.
- Original figure by Julien Coyne. Licensed CC BY-SA 4.0. Provided by: Julien Coyne License: CC BY-SA: Attribution-ShareAlike.
- Allowed mapping for a function. Provided by: Wikibooks License: CC BY-SA: Attribution-ShareAlike.
- Original figure by Julien Coyne. Licensed CC BY-SA 4.0. Provided by: Julien Coyne License: CC BY-SA: Attribution-ShareAlike.
- Original figure by Julien Coyne. Licensed CC BY-SA 4.0. Provided by: Julien Coyne License: CC BY-SA: Attribution-ShareAlike.
- square root. Provided by: Wikipedia License: CC BY-SA: Attribution-ShareAlike.
- Rational function. Provided by: Wikipedia License: CC BY-SA: Attribution-ShareAlike.
- Boundless. Provided by: Boundless Learning License: CC BY-SA: Attribution-ShareAlike.
- polynomial. Provided by: Wiktionary License: CC BY-SA: Attribution-ShareAlike.
- Original figure by Julien Coyne. Licensed CC BY-SA 4.0. Provided by: Julien Coyne License: CC BY-SA: Attribution-ShareAlike.
- Allowed mapping for a function. Provided by: Wikibooks License: CC BY-SA: Attribution-ShareAlike.
- Original figure by Julien Coyne. Licensed CC BY-SA 4.0. Provided by: Julien Coyne License: CC BY-SA: Attribution-ShareAlike.
- Original figure by Julien Coyne. Licensed CC BY-SA 4.0. Provided by: Julien Coyne License: CC BY-SA: Attribution-ShareAlike.
- Original figure by Julien Coyne. Licensed CC BY-SA 4.0. Provided by: Julien Coyne License: CC BY-SA: Attribution-ShareAlike.
- 600px-RationalDegree3.svg.png. Provided by: Wikipedia Located at: https://commons.wikimedia.org/wiki/File:RationalDegree3.svg. License: Public Domain: No Known Copyright.
- Original figure by Julien Coyne. Licensed CC BY-SA 4.0. Provided by: Julien Coyne License: CC BY-SA: Attribution-ShareAlike.
- Square Root Function Graph. Provided by: Wikipedia License: CC BY-SA: Attribution-ShareAlike.
