We've updated our
Privacy Policy effective December 15. Please read our updated Privacy Policy and tap

Study Guides > Mathematics for the Liberal Arts

Perimeter and Area

Perimeter

Perimeter is a one-dimensional measurement that is taken around the outside of a closed geometric shape. Let’s start our discussion of the concept of perimeter with an example.

Guided Example

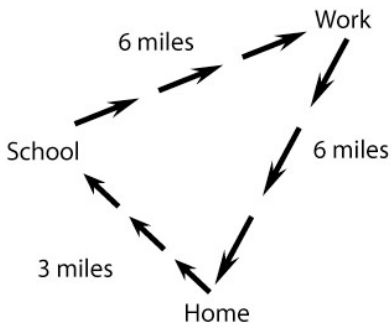
Figure 1. Figure 1.
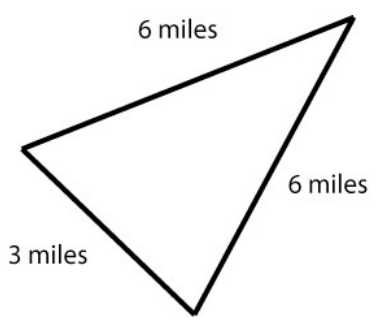
Figure 2. Figure 2.
Joseph does not own a car so must ride the bus or walk everywhere he goes. On Mondays, he must get to school, to work, and back home again. His route is pictured in figure 1. The obvious question to ask in this situation is, “how many miles does Joseph travel on Mondays”? To compute, we each distance: 3 + 6 + 6 = 15. Joseph travels 15 miles on Mondays. Another way to work with this situation is to draw a shape that represents Joseph’s travel route and is labeled with the distance from one spot to another. Notice that the shape made by Joseph’s route is that of a closed geometric figure with three sides (a triangle) (see figure 2). What we can ask about this shape is, “what is the perimeter of the triangle”? Perimeter means “distance around a closed figure or shape” and to compute we add each length: 3 + 6 + 6 = 15 Our conclusion is the same as above: Joseph travels 15 miles on Mondays. However, what we did was model the situation with a geometric shape and then apply a specific geometric concept (perimeter) to computer how far Joseph traveled.

Notes on Perimeter

  • Perimeter is a one-dimensional measurement that represents the distance around a closed geometric figure or shape (no gaps).
  • To find perimeter, add the lengths of each side of the shape.
  • If there are units, include units in your final result. Units will always be of single dimension (i.e. feet, inches, yards, centimeters, etc…)
To compute perimeter, our shapes must be closed. Figure 3 shows the difference between a closed figure and an open figure.
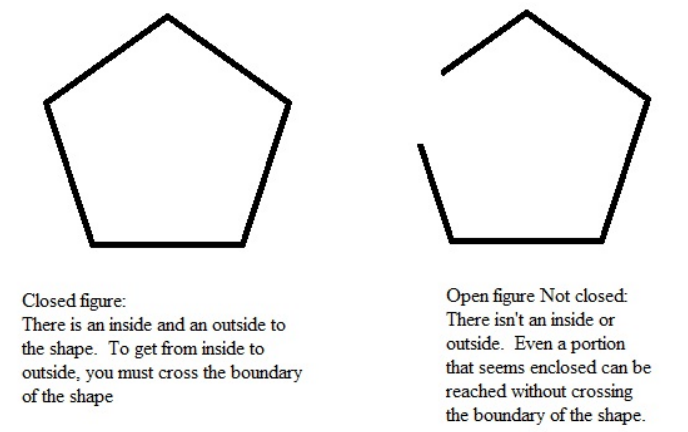
Fig2_2_3 Figure 3.

Example 1

Find the perimeter for each of the shapes below.
  1. Add the lengths of each side. Fig2_2_4
  2. Sometimes you have to make assumptions if lengths are not labeled. Fig2_2_5

Solutions

  1. 12 units
  2. 40 feet

Example 2

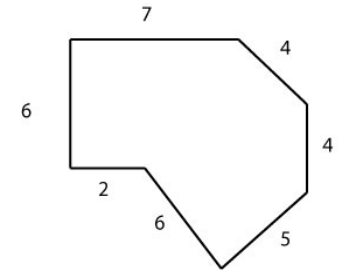
How do we find the perimeter of this more complicated shape? Fig2_2_6

Solution

Just keep adding those side lengths. 6 + 7 + 4 + 4 + 5 + 6 + 2 = 34 units
If you look closely at the shapes in the previous examples, you might notice some ways to write each perimeter as a more explicit formula. See if the results from what we have done so far match the formulas below.
Shape Perimeter
Triangle with side lengths, a, b, c: Fig2_2_7 [latex]P=a+b+c\\[/latex]
Square with side length a:  Fig2_2_8  [latex]P=a+a+a+a\\[/latex] [latex]P=4a\\[/latex]
Rectangle with side lengths a, b: 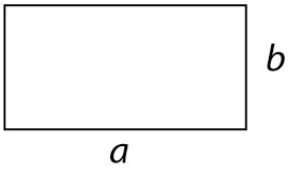Fig2_2_9  [latex]P=a+b+a+b\\[/latex] [latex-display]P=a+a+b+b\\[/latex-display] [latex]P=2a+2b\\[/latex]

Circumference

You may realize that we have not yet discussed the distance around a very important geometric shape: a circle! The distance around a circle has a special name called the circumference. To find the circumference of a circle, we use this formula: C = 2πr
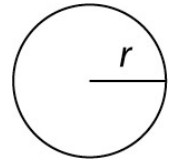
Figure 4. Figure 4.
In this formula, π is pronounced “pi,” and is defined as the circumference of a circle divided by its diameter: [latex]\displaystyle\pi=\frac{C}{d}\\[/latex]. We usually replace π with the approximation 3.14. The letter r represents the radius of the circle. Let’s see where the formula for circumference comes from. Figure 4 shows a generic circle with radius r.

Notes about C = 2πr

Remember that in the formula, when computing the circumference C = 2πr, we multiply as follows usually substituting 3.14 in place of π:

C = 2 × 3.14 × r

Often, the use of ( ) will help make the different parts of the formula easier to see:

C = (2)×(3.14)×(r)

Origins of C = 2πr

As mentioned earlier, the special number π is defined as the ratio of a circle’s circumference to its diameter. We can write this in equation form as: [latex]\displaystyle\frac{C}{d}=\pi\\[/latex] We know from our previous work that to identify the unknown, C, we can move d to the other side of the equation by writing C = πd. The diameter is all the way across the circle’s middle so the diameter is twice the radius. We can update C in terms of the radius as C = π(2r). With a little final rearranging of the order our parts are written in, we can say that C = 2πr. Let’s use the formula to find the circumference of a few circles.

Example 3

Find the circumference of each of the following circles. Leave your answers first in exact form and then in rounded form (to the hundredths place). (Note that when a radius is given, its value is centered above a radius segment. When a diameter is given, its value is centered above a diameter segment.)
  1. Fig2_2_11
  2. Fig2_2_12

Solutions

  1. Exact 8π in; rounded from exact answer 25.13 in; rounded using 3.14 for π 25.12 in
  2. Exact 12.44π m; rounded from exact answer 39.08 m; rounded using 3.14 for π 39.06 m

Exact Form vs. Rounded Form

  • π is a number in exact form. It is not rounded.
  • 3.14 is a rounded form approximation for π
Why does it matter which form we use? It matters because when we round, we introduce error into our final result. For this class, that error is usually acceptable. However, you will find in other subjects such as physics or chemistry, that level of accuracy is a concept of great importance. Let’s see an example of the difference in forms.

Example 4

The radius of the moon is about 1079 miles. What is the circumference? Let's solve this using both the exact form and the rounded form:

Exact Solution

[latex-display]C=2\pi{r}= 2\pi(1079)=2158\pi\\[/latex-display] To round from the exact solution, use the π button on your calculator to get [latex-display]2158\pi\approx6779.56\\[/latex-display]

Rounded Solution

[latex-display]C=2\pi{r}= 2(3.14)(1079)\approx6776.12\\[/latex-display] Notice that our final results are different. That difference is the error created by using 3.14 as an initial approximation for π. When doing homework and tests, read the directions carefully on each problem to see which form to use.

Example 5

Find the circumference or perimeter given in each described situation below. Include a drawing of the shape with the included information. Use the examples to help determine what shapes to draw. Show all work. As in the examples, if units are included then units should be present in your final result. Round to tenths unless indicated otherwise.
  1. Find the perimeter of a square with side length 2.17 feet.
  2. Find the perimeter of a rectangle with sides of length 4.2 and 3.8.
  3. Find the perimeter of a triangle with sides of length 2, 5, 7.
  4. Find the circumference of a circle with radius 6 inches. Present answer in exact form and also compute using 3.14 for π. Present rounded form to the nearest tenth.
  5. Find the circumference of a circle with diameter 14.8 inches. Present answer in exact form and also compute using 3.14 for π. Present rounded form to the nearest tenth.

Solutions

  1. 8.68 feet
  2. 16
  3. 14
  4. Exact 12π in, Rounded 37.7 in
  5. Exact 14.8π in, Rounded 46.5 in

Example 6

Finding the Distance around Non-Standard Shapes

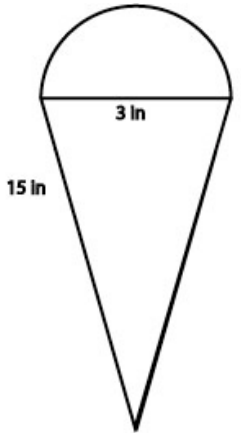
The basic formulas for perimeter of straight-line shapes and the circumference of a circle will help us find the distance around more complicated figures. Find the distance around the following shape. Round final answer to tenths and use 3.14 for π. Fig2_2_13

Solution

34.7 in

Example 7

Applications of Perimeter and Circumference

Our knowledge of basic geometric shapes can be applied to solve "real-life" problems. Wally wants to add a fence to the back of his house to make some room for his children to play safely (see diagram below). He began measuring his yard but got distracted and forgot to finish measuring before he went to the store. If he remembers that the back wall of his house is 15 yards long, does he have enough information to buy the fencing he needs? If so, how many feet should he buy? Fig2_2_14

Solution

81 feet

Area

Let’s take another look at Wally’s backyard from Example 7 in order to introduce the next concept: area.

Guided Example

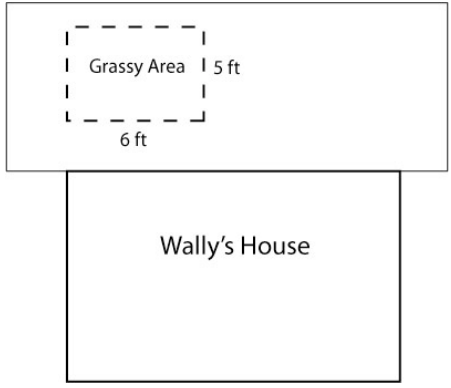
Wally successfully fenced his yard but now wants to add some landscaping and create a grassy area as shown below. Fig2_2_15 He heads down to the local lawn store and finds out that in order to determine how much sod he needs, he must figure out the square footage of the area he wants to add grass to. On his way home, he realizes that if he divides the grassy area into sections that are 1 foot by 1 foot and then counts them, he can determine the square footage. Here is the information Wally drew up when he got home. Fig2_2_16 Wally correctly determined the area of the rectangular grassy section to be 30 square feet.

Notes on Area

  • Area is a two-dimensional measurement that represents the amount of space inside a two-dimensional shape.
  • To find the area, count the number of unit squares inside the shape.
  • If there are units, include units in your final result. Units will always be two-dimensional (i.e. square feet, square yards, square miles, etc…)

Example 8

Find the area for each of the shapes below.
  1. Remember to count the unit squares inside the shape. Fig2_2_17
  2. Is there a pattern here that would make our work easier? Fig2_2_18

Example 9

How do we find the area for shapes that are more complicated? Break up the areas into shapes that we recognize and add the area values together. Fig2_2_19
If you look closely at the shapes in the previous examples, you might notice some ways to write each area as a more explicit formula. See if the results from what we have done so far match the formulas below.
Shape Area
Square with side length a Fig2_2_8 [latex]A=a\cdot{a}\\[/latex] [latex]A=a^2\\[/latex]
Rectangle with side lengths a, b Fig2_2_9 [latex-display]A=a\cdot{b}\\[/latex-display] (You will also see this as [latex]A=\text{length}\cdot\text{width}\\[/latex])
The area formulas for the shapes below are more complicated to derive so the formulas are listed for you in the table.
Shape Shape
Triangle with height h and base b Fig2_2_20 [latex-display]\displaystyle{A}=\frac{1}{2}bh=\frac{bh}{2}\\[/latex-display] Read as “one-half base times height” Note that h is the straight-line distance from top of the triangle directly to the other side. The small box next to h indicates this. In math terms the box indicates a 90º (right) angle. Circle with radius r Figure 4. [latex-display]A=\pi{r}^2\\[/latex-display] Read as “pi times radius squared”
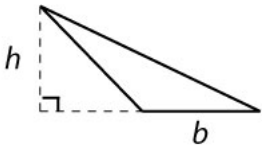Fig2_2_21 If your triangle is as pictured at left, then the height is drawn and measured outside the triangle. The area formula is the same.

Example 10

Find the area for each described situation. Create a drawing of the shape with the included information. Show all work. As in the examples, if units are included then units should be present in your final result. Use 3.14 for π and round answers to tenths as needed.
  1. Find the area of a rectangle whose length is 12.9 meters and height is one-third that amount.
  2. Find the area of a triangle with base [latex]\displaystyle{24}\frac{1}{2}\\[/latex] inches and height 7 inches.
  3. Find the area of a circle with radius [latex]\displaystyle{2}\frac{1}{3}\\[/latex] inches. Present answer in exact form and also compute rounded form using 3.14 for π. Present rounded form to the nearest tenth.

Solutions

  1. 55.5 m2 or 55.5 square meters (rounded)
  2. 85.8 in2 or 85.8 square inches (rounded)
  3. Exact 49/9 π in2, Rounded 17.1 in2

Example 11

Find the area given each described situation. Include a drawing of the shape with the included information. Show all work. As in the examples, if units are included then units should be present in your final result. Round answers to tenths unless otherwise indicated.
  1. Find the area of a square with side length 4.2 feet.
  2. Find the area of a rectangle with sides of length 4.2 and 3.8.
  3. Find the area of a triangle with height 7 inches and base 12 inches.
  4. Find the area of a circle with radius 6 inches. Present answer in exact form and also compute using 3.14 for π. Present rounded form to the nearest tenth.

Solutions

  1. 17.64 ft2 or 17.64 square feet
  2. 16.0
  3. 42 in2 or 42 square inches
  4. Exact 36π in2 or 36π square inches, Rounded using 3.14 for π 113.0 in2 or 113.0 square inches

Example 12

Finding the Area of Non-Standard Shapes

The basic formulas for area will help us find the area of more complicated figures. This is the same problem we found the perimeter for earlier. Find the area of the given shape. Compute using 3.14 for π and round to the nearest tenth. Fig2_2_22

Solution

Rounded using 3.14 for π 25.9 in2

Example 13

Applications of Area and Perimeter

We can combine our knowledge of area/perimeter to solve problems such as this one. Wally is still fixing up his house and has a flooring project to complete. He wants to buy enough bamboo flooring to cover the floor space in rooms A, C and hallway B and enough bamboo edging for baseboards in all the spaces as well. How many square feet of flooring and how many feet of baseboards should he buy? Fig2_2_23

Solution

256 ft2 flooring, 108 ft edging

Licenses & Attributions

CC licensed content, Shared previously

  • Basic Arithmetic Student Workbook. Provided by: Scottsdale Community College Authored by: Donna Gaudet, Amy Volpe, and Jenifer Bohart. Located at: https://sccmath.wordpress.com/. License: CC BY-SA: Attribution-ShareAlike.