H1.05: Example 3 Alternative Method
Alternative method of solution for Example 3:
Example 3 question: For a certain type of letter sent by Federal Express, the charge is $8.50 for the first 8 ounces and $0.90 for each additional ounce (up to 16 ounces.) How much will it cost to send a 12-ounce letter? We saw here that it is awkward for the value to be so far from any useful values for the variables. This suggests that we re-define the variables to be more useful. 1-2. Define the variables and their units and possible values. List the points. Let x = number of ounces above 8. So the possible values for x are 0 to 8 (which corresponds to the letter weighing 8 ounces to 16 ounces.) Let y = cost. The possible values for y are $8.50 and larger. A letter weighing 8 ounces costs $8.50. So x = 0. The point is (0, 8.50) A letter weighing 9 ounces costs $8.50+0.90 = $9.40. So x = 1. The point is (1, 9.40) 3. Is a linear model appropriate? Yes, because the cost increases by the same amount for each additional ounce. 4-5. Find the slope and the formula. Using the points above, we have 6. Interpret the y-intercept. When x = 0, the value for y is 8.50. Since x = weight – 8 ounces, that means that when the letter weighs 8 ounces, the cost is $8.50. Notice that defining the x-variable in this manner has made the y-intercept more meaningful in the problem. 7. Make the prediction. If the letter weighs 12 ounces, then we use x = 12 – 8 = 4. So [latex]y=8.50+0.90\cdot4=8.50+3.60=12.10[/latex]. This agrees with the answer we found by the first method. 8. Graph and check whether you obtain the same results.| weight | x = weight - 8 | y=cost |
| 8 | 0 | 8.5 |
| 9 | 1 | 9.4 |
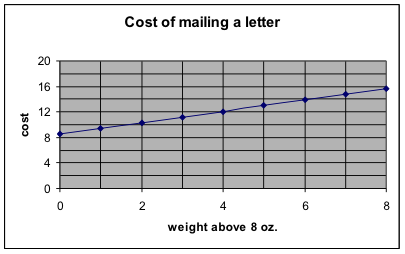 On the graph, look up a weight of 12 ounces, which is
x = 12 – 8 = 4.
The cost for x = 4 is a little larger than $12, which is consistent with the value we obtained from the formula.
On the graph, look up a weight of 12 ounces, which is
x = 12 – 8 = 4.
The cost for x = 4 is a little larger than $12, which is consistent with the value we obtained from the formula.Licenses & Attributions
CC licensed content, Shared previously
- Mathematics for Modeling. Authored by: Mary Parker and Hunter Ellinger. License: CC BY: Attribution.
